Dystrybuanta Karo: Na ospę można nie zachorować albo tylko raz. Badania w pewnym regionie dowiodły, że 94% populacji przebyło tę chorobę. Dla zmiennej losowej X zdefiniowanej jako liczba zachorowań na osobę u losowo wybranej osoby z tego regionu, obliczyć dystrybuantę i wartość oczekiwaną.

Aga1.: Spróbuję rozwiązać, ale ktoś powinien sprawdzić. Jest to zmienna typu skok0wego P[X=0]=0,06 P[X=1]=0,94 Wartość oczekiwana EX=0*0,06+1*0,94=0,94 Dystrybuanta F(x)=0,gdy x∊(−∞,0> 0,06 , x∊(0,1> 1, x∊(1,∞)

Karo: a czy w tej dystrybuancie nie powinno być na końcu 0,94, x∊ (1,∞) ?

Aga1.: Na początku jest zawsze F(x)=0, a na końcu zawsze F(x)=1i zawsze z prawej strony przedział domknięty, a z lewej otwarty.

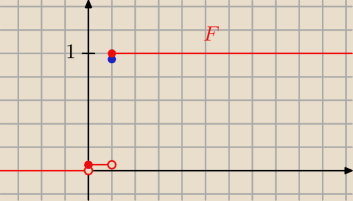
Trivial: Aga1, Twoja dystrybuanta ma źle domknięte przedziały. Powinno być: { 0 dla x∊(−∞,0) F(x) = { 0.06 dla x∊[0, 1) { 1 dla x∊[1,+∞) Niebieskie kropki (dla X = 0 pokrywa się z czerwoną) to prawdopodobieństwa dla X=0 oraz X=1.

Trivial: Właściwie zależy to od definicji dystrybuanty. U Ciebie jest zdefiniowana tak: F(x) = P(X < x) U mnie tak: F(x) = P(X ≤ x) Z tego co sobie przypominam, to obie wersje są OK, o ile ma się świadomość, której się używa, także przepraszam za pochopne osądzanie.