geometria zadanie: 1. Czy istnieje trójkat, którego wysokosci maja długosci a) 5, 5, 11 ; b) 5, 5, 3 ; c) 5, 5, 9 ; d) 5, 5, 2 ? jezeli 2 wysokosci w trojkacie sa rownej dlugosci to czy taki trojkat nie jest rownoramienny? 2. Czy istnieje czworoscian, którego wysokosci maja długosci a) 5, 5, 5, 4 ; b) 5, 5, 5, 2 ; c) 5, 5, 5, 16 ; d) 5, 5, 5, 1 ?

zadanie: 1. h_a=5=h_b h_c=11

1		1
	*a*ha=		b*hb
2		2

5a=5b b=a a*h_a=c*h_c 5a=11c 11c=5a

	5
c=		a
	11

	5
w trojkacie a+b>c czyli a+a>		a
	11

	5
2a>		a
	11

	5
2>
	11

odp. tak istnieje taki trojkat dobrze?

zadanie: a co z czworoscianem?

PW: Spróbuj poprzez objętość (poprzedni sposób można nazwać "poprzez pole").

Mila: 1) Jeżeli dwie wysokości w trójkącie są równej długości to trójkąt jest równoramienny. 2) W trójkącie, badasz, czy suma długości dwóch krótszych boków jest większa od długości trzeciego boku.

	5
a+		a>?a
	11

	5
1		>1
	11

odp. Tak 3) W następnym zadaniu , tak, jak radzi PW.

zadanie: dziekuje a jaki jest warunek na istnienie czworoscianu?

zadanie: czyli ze wzoru na objetosc czworoscianu V=U{1}[3}*P_p*H P_p=U{1}[2}*a*h_a a czy jezeli 3 wysokosci czworoscianu sa rownej dlugosci to czy ten czworoscian jest jalis szczegolny w sensie skladajacy sie ze scian o trojkatach rownoramiennych badz innych? a*h_a*H_a=b*h_b*H_b a*h_a*5=b*h_b*5 a*h_a=b*h_b czy wysokosci h_a i h−b sa rowne? wtedy a=b jaki jest warunek na istnienie czworoscianu?

zadanie: ?

Mila: Wg mnie jest to ostrosłup prawidłowy trójkątny. Porównaj objętości:

1		a2√3		1
	*		*H=		a*hb*h, [h=5,H=4 w przykładzie (a)]
3		4		2

oblicz z tego a, ma wyjść dodatnie, h_b − liczysz z tw. Pitagorasa. Wyprowadziłam wzór ogólny, ale jeszcze sprawdzam i myślę nad innym sposobem. Policz wg tego sposobu.

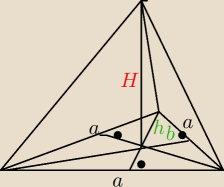
zadanie: dobrze tylko mam pytanie do tego wzoru bo po lewej stronie jest wzor na objetosc a po prawej? jezeli tez na objetosc to czemu nie ma U{1}[3}? i jak pada wysokosc h? bo przeciez musi sie to sobie rownac?

zadanie: tylko tak sie teraz zastanawiam, ze h_b to wysokosc w trojkacie rownoramiennym bo prawa strona to pole trojkata rownoramiennego? bo na poczatku myslalem, ze rownobocznego ale skoro a*h_b

zadanie:

	1
ale i tak nie wiem co z tym		?
	3

Mila:

	1
Zapomniałam o		z prawej.
	3

h_b to wysokość ściany bocznej. Po kolacji, napiszę więcej. h to wysokość ostrosłupa poprowadzona do ściany bocznej i nie interesuje Cię gdzie pada.

1		1
	*Pp*H=		*Sb*h
3		3

S−b − pole ściany bocznej. Masz odpowiedzi?

zadanie: a) tak b) tak c) tak d) nie

Mila: Mam warunek z porównania objętości: (postaraj się wyprowadzić) 9H²>h²⇔

	h
H>
	3

	5
a) H=4>		tak
	3

	5
b) H=2>		tak
	3

	5
c)H=16>		tak
	3

	5
d)1<		nie
	3

zadanie:

	3a2		576+3a2
hb2=16+		=
	36		36

	√3a2+576
hb=
	6

1		√3a2+576
	*a*		*5=a2√3/:a
2		6

√3a2+576
	*5=a√3/*12
12

5(√3a²+576)=12a√3/()² 25(3a²+576)=432a² 75a²+14400=432a² 357a²=14400/:3 119a^a=4800

	4800
a2=
	119

	40√357
a=
	119

chyba dobrze?

Mila: Nie licz za każdym razem, wyprowadź wzór na ogólnych danych. Wiem, że potrafisz. Jeśli Ci nie wyjdzie, to nie wyrzucam kartki, napiszę. Niepotrzebnie liczysz a do końca, ma wyjść >0, bo to oznacza, że ścianki boczne nie "zwiną" się na podstawę.

zadanie:

1		a2√3		1		1
	*		*H=		*		*a*hb*h
3		4		3		2

a2√3		1
	*H=		*a*hb*h /*4
4		2

a²√3*H=2ah_b*h/ :a a√3*H=2h_b*h /()² 3a²*H²=4h_b²h²

	576+3a2
3a2H2=4h2*		/ *36
	36

108a²H²=4h²*(576+3a²) 108a²H²=2304h²+12a²h² 9a²H²−a²h²−192h²=0 a²(9H²−h²)=192h²

	192h2
a2=
	9H2−h2

a² nie moze byc rowne liczbie ujemnej wiec mianownik musi byc wiekszy od zera (licznik jest wiekszy od zera) czyli 9H²−h²>0 9H²>h² 3H>h /:3

	h
h>
	3

dobrze?

zadanie:

	h
H>
	3

zadanie: ?

Mila: I teraz sprawdzasz tylko ten warunek.

zadanie: dziękuje

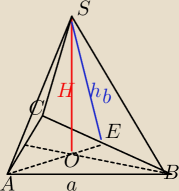
Mila: Mój licznik jest trochę inny.

	1		a2
hb2=(		a√3)2+H2=		+H2
	6		12

a2√3		1
	*H=		a*hb*h /*4
4		2

a²√3*H=2a*h_b*h / :a a√3*H=2h_b*h /²

	a2
3a2*H2=4*h2*(		+H2)
	12

	h2*a2
3a2*H2=		+4h2*H2
	3

	h2*a2
3a2*H2−		=4h2*H2
	3

9a2*H2−h2*a2
	=4h2*H2
3

9a²*H²−h²*a²=12h²*H²

	12H2*h2
a2=
	9H2−h2

9H²>h²

	h2
H2>		, H>0 i h>0
	9

	h
H>
	3

zadanie: dziekuje