Najkrótsza odległość. Funkcje. Pochodne. V.Abel: Witam! Proszę o pomoc (podpowiedź, najlepiej wyjaśnienie ):

	1
Dany jest wykres funkcji f(x)=		x2 oraz punkt P=(5,1), Znajdź punkt należący do wykresu
	2

funkcji f, który jest najbliżej punktu P. Bardzo proszę o pomoc

sushi_ gg6397228: niech A nalezy do paraboli A(x; 0,5 x²) P(5;1) policz długośc odcinka AP bedzie funkcja od x oraz minimum

V.Abel: ok, a można spróbować tak(?): 1. policzyć pochodną f(x) jako współczynnik stycznej do paraboli 2. równanie stycznej przekształcić w postać ogólną prostej 3. wstawić pkt 2. oraz P(5,1) do wzoru na odległość punktu od prostej 4. z pkt.3 mam funkcję zależną od x 5. NIE WYCHODZI (dlaczego)?

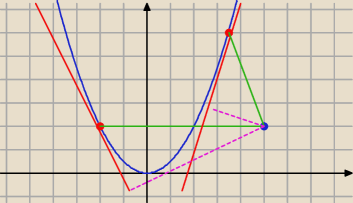
Basia: szukasz minimum tego co jest na zielono odległość P od paraboli = odległość P od punktu na paraboli ≠ odległość P od stycznej do paraboli w tym punkcie (fioletowe)

V.Abel: Basia, dlaczego? Nie mogę uznać, że szukany punkt na paraboli należy do stycznej do paraboli w tym punkcie?

V.Abel: aha, już wiem czy jest jeszcze inny sposób niż ten, który podpowiedział sushi_gg63972228 ?

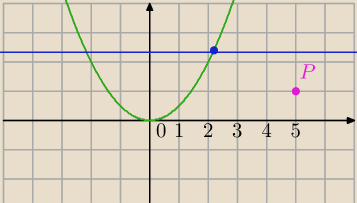
Mila: To zadanie z LO, czy studiów? d=√(x−5)²+(0,5x²−1)² d²=g(x)=(x−5)²+(0,5x²−1)² (g(x))'=2(x−5)+2*(0,5x²−1)*x g'(x)=x³−10 x³−10=0 x=³√10

	1
f(3√10)=		3√100
	2

	3√100
Q=(3√10;		)
	2

PW: "Stycznej do paraboli w tym punkcie" to znaczy w którym (mówisz o pierwszej współrzędnej jakiego punktu)?

Basia: nie widzę innego sposobu

V.Abel: Mila − zadanie z LO (stara ustawa programowa) PW − chodzi mi o to, czy nie da się zrobić tak, że punkt na paraboli, potraktować jako punkt, który należy do stycznej do paraboli właśnie w tym punkcie, wiesz o co mi chodzi (mam nadzieję)

V.Abel: ale w sumie tak nie można, bo gwarancji nie ma, że to ten punkt, Basia pokazała − ok, wiem. Dzięki Wszystkim ps serio nie da się inaczej?

Basia: punkt A(x₀,y₀) leżący na paraboli należy do stycznej do paraboli w p−cie x₀ ale odległość P od punktu A ≠ odległości P od tej stycznej narysowałam Ci to

V.Abel: Wiem właśnie, już zauważyłem − dzięki za pomoc

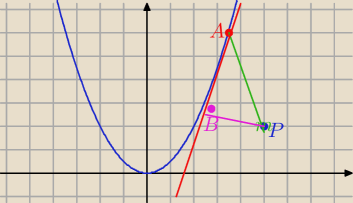
Basia: masz badać |AP| (zielone) a odległość P od stycznej w p−cie A to |PB| (fioletowe) teraz lepiej widać ?

V.Abel: Widać, widać, wcześniej też było Już mam − dzięki wielkie za powtórną fatygę