geometria analityczna matma: Punkty A (−1,3), B (−2,0), C (2,−3) są kolejnymi wierzchołkami równoległoboku ABCD. Oblicz współrzędną wierzchołka oraz pole tego równoległoboku.

wredulus_pospolitus: krok 1 wyznaczasz prostą przechodzącą przez punkty A i B krok 2 wyznaczasz prostą równoległą do prostej z kroku 1 ... ale przechodząca przez punkt C krok 3 wyznaczasz prostą przechodzącą przez punkty B i C krok 4 wyznaczasz prostą równoległą do prostej z kroku 3 ... ale przechodząca przez punkt A krok 5 wyznaczasz punkt przecięcia się prostych z kroku 2 i 4 krok 6 to jest własnie wierzchołek D

Bogdan:

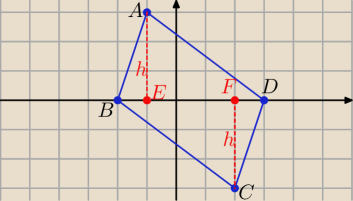
	−1+2		3−3		1
S = (		;		) = (		; 0)
	2		2		2

	1
xD + (−2) = 2*		⇒ xD = 3, yD + 0 = 2*0 ⇒ yD = 0, D = (3, 0)
	2

Wykorzystując warunki zadania wyznaczamy: E = (−1, 0), F = (2, 0) |BD| = |−2 − 3| = 5, h = |AE| = |3 − 0| = 3 oraz h = |FC| = |0 − (−3)| = 3

	1
Pole równoległoboku P = 2 *		*|BD| * h = 5 * 3 = 15
	2

Bogdan: S − punkt przecięcia przekątnych