Zadania Tone: Witam ponownie , próbowałem się z tym uprać ale nie mogę coś mi nie wychodzi , źle podstawiam czy co 1.Liczba x jeden jest pierwiastkiem równania x²−2010x−2011=0 Wobec tego liczba x²i na dole 1 −2010x 1 − 2010 jest równa te jedynki to w indeksie dolnym tak jak tam napisałem słowami na początku 2. x²+9>0 i to samo działanie tylko że z minusem liczyłem delta ale jakieś pierdoly wychodzą nie mogę już pomocy! 3. (x−5)²>0 nie jest liczba ma wyjść √5 ale postawiłem do wzoru skróconego mnożenia potem wyliczyłem deltę delta mi wyszła 0 wiec stosuje się do tego wzrou Δ=− b przez 2*a czyli i z tego mi wyszło −10 i Jeżeli ktoś ma czas podpowiedzieć chociaż do bardzo bym prosił

Mila: W ogóle nie mogę zrozumieć o co Ci chodzi. Przepisz dokładnie zadania z poleceniami.

Tone: OK

Tone: przepiszę 2, 3 bo w 1 za dużo pisania 2. x²+9>0 nie mogę coś wyliczyć delty bo głupoty wychodzą , i mam taki sam drugi przykład tyko z minusem 3. (x−5)^>0 zastosowałem wzór skróconego mnożenia ale nie mogę coś wyliczyć z delty bo wychodzi mi 0

Tone: 1. Liczba x₁ jest pierwiastkiem równania x² − 2010x−2011=0 Wobec tego liczba x²₁ −2010x₁ − 2010 jest równa

wredulus_pospolitus: 2. zauważ, że x² ≥ 0 dla dowolnego 'x' ... prawda ?! więc x²+9 będzie większe od zera (dla dowolnego 'x') ... i dlatego Δ wychodzi Ci ujemna −−−− brak miejsc zerowych

wredulus_pospolitus: (x−5)² > 0 ... a po co z tej postaci widzisz 'miejsce zerowe' kiedy (coś)² NIE BĘDZIE większe od 0

Tone: no właśnie tak myślałem że brak miejsc zerowych bo tak mi wychodziło to chyba w książce w rozwiązaniach jest błąd.

Tone: w tym x²+9>0

wredulus_pospolitus: x²+9 <−−− brak miejsc zerowych x² − 9 = (x−3)*(x+3) <−−− wzór skróconego mnożenia

Tone: no właśnie nie jestem taki mądry jak ty więc wyliczyłem i wyszło mi − delta czyli nie ma miejsc zerowych

wredulus_pospolitus: dlaczego bzdury x²+9>0 => x∊R (czyli dla kazdego 'x')

Tone: podam ci jak jest w rozwiązaniu

Tone: z tego x²+9>0 ma wyjść 1 tak pisze w odpowiedzi w książce dlatego tak się zastanawiam co robię źle

Tone: dla jasności to zadania zamknięte czyli tam jest tak , podam cała treść Najmniejszą liczbą całkowitą dodatnią spełniającą nierówność x²+9>0 jest : A. 1 B.3 C−3 D−1

Tone: aha czyli w tym x²−9 mam zapisać w prostej postaci i dopiero wzór skróconego mnożenia zastosować jeżeli dobrze rozumiem

Tone: ?

Tone: A wracając do tego x²+9 to jak nie ma miejsc zerowych to prawidłowa odpowiedz to 1 ?

wredulus_pospolitus: no to chłopie KAZDA liczba całkowita dodatnia spełnia to równanie ... więc najmniejszą liczbą naturalną dodatnią spełniającą to równanie jest '1'

Tone: Jeszcze bym prosił o udzielenie podpowiedzi na Zadanie 1 , bo tam nie mogę się połapać już w ogóle ale jestem tępy

Tone: A no faktycznie że odpowiedz A no teraz już coś zrozumiałem dziękuję!

Tone: Chce się tego bardzo nauczyć kurde ale co zrobię dobrze zadanie inne to już z drugim mam problem

Tone: a wydawało się to takie proste że jak już widzę , że x² −9>0 to b nie ma x czyli już adekwatnie kieruje się że b =0 a c=9 i a=1 a jednak przeliczyłem się .

Tone: wredulus tylko wytłumacz mi jak z x²−9 jest (x−3)*(x+3) przyrównujemy to do zera i wtedy otrzymam z tego taką postać ?

wredulus_pospolitus: no i dobrze kieruje się ale też możesz (wyższa szkoła jazdy) zauwazyć że to jest wzór skróconego mnożenia: (a²−b²) = (a−b)*(a+b)

Tone: Proszę naprawdę chcę to zrozumieć .

wredulus_pospolitus: x² − 2010x − 2011 = 0 jednym z rozwiązań tego równania jest x₁ w takim razie: (x₁)² − 2010x₁ − 2011 = 0 dlaczego BO JEST ROZWIĄZANIEM TAMTEGO RÓWNANIA przykład: x+3 = 2 <−−− rozwiązaniem tego równania jest x₁ = −1 a więc: x₁ + 3 = −1 + 3 = 2

Tone: no dobrze można to zastosować ale jeżeli jest x²−9>0 to jak tutaj zastosuje (a²−b²)=(a−b)*(a+b) jeżeli mój współczynnik b nie jest podniesiony do kwadratu

wredulus_pospolitus: a² = x² −> a = x b² = 9 −> b = √9 = 3

Tone: aha czyli w zadaniu 1 . prawidłowa odpowiedz to 1

Mila: x²−9=x²−3²=(x−3)*(x+3)

Tone: aha i dlatego potem zamieniam w na tą postać ze wzoru czyli (x−3)*(x+3)

Tone: Aha @mila czyli można też to tak

Tone: Dziękuję bardzo za wytłumaczenie

Tone: Teraz zauważyłem , że nie jasne jest dla mnie po tym co mam zrobić czy mam to pomnożyć , przez oba nawiasy czy przyrównać do 0

Tone: i jak pomnożę to liczyć deltę ?

Tone: Bo w zadaniu jest napisane największa liczbą spełniająca nierówność x²−9>0 jest A:−9 b:−4 c:−3 d:−1

Tone: musi mi wyjść −4 a jeżeli przyrównam do 0 to wychodzi −3

Tone: Proszę olśnijcie mnie

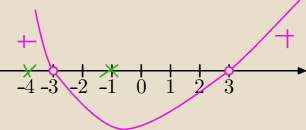
Mila: Z podanych liczb nierówność: (x²−9)>0 spełniają liczby −9,−4 −4>−9 odp.−4

Tone: aha <thank you so much>

Mila:

Tone: no dobrze to rozumiem ale jeżeli miałem tam wcześniej (x−3)*(x+3) to jak widzę ze wzoru przyrównałaś do 0 i narysowałaś oś funkcji tak , i w odpowiedzi mam też −3 to dlaczego nie −3 bo należy już do tego przedziału czy jak ?

Tone: Sory że tak mące ale chcę to zrozumieć , i tak płacę jeszcze za korki z matmy a i tak niektórych zadań nie mogłem zrozumieć jak doszło do jego rozwiązania dlatego się pytam nie jestem typem co szuka gotowca tylko chcę to zrozumieć żeby polubić tą matematykę

Tone: no bo tam jest tak (x−3)(x+3) czyli potem piszę x−3=0 lub x+3=0 z czego wychodzi x=3 i x =−3 dlaczego nie może być w odpowiedzi −4 tego nie mogę zrozumieć bo przecież −3 jest większe od −4 ?

Tone: dlaczego musi być "−4" mój błąd przecież −4 to poprawna odpowiedz błędnie napisałem poprawiam ::""

Tone: Może już to zrozumiem już dość mi pomogłaś zrozumieć , nie zabieram ci czasu pa .

Mila: liczba (−3) nie spełnia nierówności (kółeczko nie jest zamalowane), przeczytaj uważnie wpis 18:13.

Tone: aha teraz już rozumiem

Tone: a jeżeli mam tutaj takie równanie x>x² to przenoszę to tak żeby uzyskać postać x²−X>0

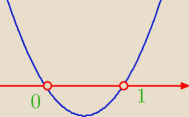
bezendu: x²−x>0 x(x−1)>0 x∊(−∞,0)∪(1,∞)

Tone: i wtedy mogę wzór skróconego mnożenia bo z delty się nie da wychodzi że Δ<0

Tone: aha czyli tak jak myślałem mogłem nie pisać czyli wyciągnąć po prostu x przez nawias o

Tone: eh i wyszedłem na idiotę

bezendu: wzór skróconego mnożenia a gdzie Ty taki widzisz ? wyciągasz x przed nawias i po kłopocie

Tone: bezendu chciał bym mieć takiego brata to by mnie nauczył wszystkiego mój młodszy brat umie matme ale jest straszliwym leniem i tyko śmieje się ze mnie , a sam marnuje swój talent −;−

Tone: za to mi bardzo ciężko mi to przychodzi chodź nie poddaje się to i tak to cholernie trudne , a to przecież jedne z najprostszych rzeczy w matematyce

Tone: No dobra nie będę ględzić tylko tutaj zapytam jak mam okazje mam taki przykład (2x+7)(x+11)<0 I Jeżeli dobrze rozumiem to mam to zrobić tak 2x+7=0 lub x+11=0 2x=−7 I :2

	−7
x= −
	2

x=−4 a w tym drugim to nie wiem co mam zrobic x= −11 i co dalej to nie wiem

Tone: x= − 3,5 przepraszam a w poleceniu mam ile jest liczb całkowitych spełniających tą nierówność

Piotr:

7
	= 4
2

no masz drugi x = −11 zaznaczasz na osi i piszesz odpowiedz.

Piotr: no i teraz wypisz wszystkie liczby calkowite z tego przedzialu i policz ile ich jest.

Piotr: hej bezendu maja byc <0

bezendu: hej Piotr no to mam x∊(−11,−3,5)

Tone: 3,5 pomyliłem się wybacz ;

Tone: czyli dobrze to rozwiązałem tylko teraz muszę wypisać liczby z tego przedziału tak ?

bezendu: tak

Piotr: jakiego koloru używać do Twojego nicku ? [pytam bezendu]

Tone: bezendu właśnie nie mogę szybciej bo nie mam takiego myślenia jak ty tylko jak ślimak '/

Tone: mówiłem już że się pomyliłem

Tone: a czego na wykresie jest 11 chyba powinno być −11 ?

bezendu: Piotr do wyboru do koloru

Piotr: powinno i powinno być na lewo od −3,5

Tone: hehe to już nie musisz wchodzić w takie szczegóły wiemy jaki będzie wynik tylko bez − ta 11 to wiesz nieraz zapomnisz jednego znaku i całe zadanie do wywalenia

Tone: bo będzie źle

Tone: ok resztę mam łatwe poradzę sobie dzięki all <3

Tone: czyli będzie 8

Tone: dziękuję bardzo jeszcze raz za kroki płace i dowiem się tyle co tutaj tylko , że na korkach idziemy działami jakie muszę umieć na maturze ostatnio jak pisałem maturę zabrakło mi 1 punkt to myślałem że się zabije ;.

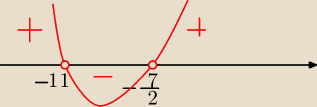
Mila: Słuszna uwaga. Zaczynasz myśleć. (2x+7)(x+11)<0 masz postać iloczynową trójmianu kwadratowego ( wykresem jest parabola skierowana do góry), liczysz miejsca zerowe: 2x+7=0 lub x+11=0 2x=−7 lub x=−11

	−7
x=		lub x=−11
	2

(2x+7)(x+11)<0 ⇔x∊(−11;−3,5)

Tone: ale to takie moje już bzdury , nie musiałem tego tutaj pisać .

Tone: Miła ty naprawdę jesteś "Miła"

bezendu: @Tone Mila

Tone: nie muszę rysować tego wykresu miałem za zadanie tylko ile licz całkowitych jest w zakresie tych liczb

Tone: dobra dobra dzięki jeszcze raz stary

bezendu: Nie jestem ''stary''...

Mila: No to ile jest tych liczb?

Piotr: nie 8 tylko 7 : −10, −9, −8, −7 , −6, −5, −4

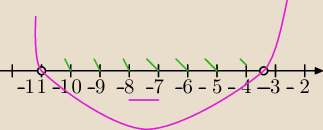Mila: Tony należy pisać całą treść zadania, do takiego problemu należało inaczej opisać oś, wtedy wszystko widać, a na maturze to będzie strata 1 punktu (wiesz co to oznacza). I jest tak, jak pisze Piotr. Nie zawsze to jest możliwe, ale jeśli można dokładnie zaznaczyć, to zaznaczamy.