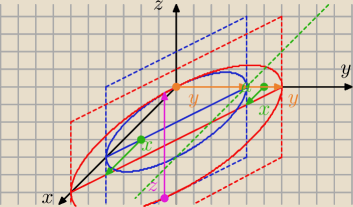
objętość efgrhtj: Znaleźć objętość bryły ograniczonej powierzchniami z²=xy,y+x=4,y+x=6. Męczę się z tym i nie wiem ale tego się nie da zrobić Tak wiem, trzeba narysować wykres, i to już mam, ale jakie granice wziąć dla y? Proszę o jasne odpowiedzi, gdyż bardzo zależy mi na czasie, bo egzamin tuż tuz.

Trivial: |Ω| = ∭_Ω dxdydz = ∫₀⁴ dy ∫_4−y^6−y dx ∫_−√xy^√xy dz + ∫₄⁶ dy ∫₀^6−y dx ∫_−√xy^√xy dz = ∫₀⁴ dy ∫_4−y^6−y 2√xy dx + ∫₄⁶ dy ∫₀^6−y 2√xy dx

	2		2
= ∫04 2√y*		[(6−y)3/2 − (4−y)3/2]dy + ∫46 2√y*		(6−y)3/2dy
	3		3

	4
=		[∫04 √y(6−y)3/2dy − ∫04 √y(4−y)3/2dy + ∫46 √y(6−y)3/2dy]
	3

	4
=		[∫06 √y(6−y)3/2dy − ∫04 √y(4−y)3/2dy]
	3

Wprowadzamy oznaczenie J(A) = ∫₀^A √y(A−y)^3/2dy

	4
I mamy: |Ω| =		(J(6) − J(4)).
	3

Pozostało znaleźć J(A). Dokonujemy podstawienia u = A−y, u(0) = A, u(A) = 0 J(A) = ∫₀^A √y(A−y)^3/2dy = +∫₀^A √A−uu^3/2du = ∫₀^A u√u(A−u)du Pozostało to doliczyć.

efgrhtj: dzięki