Układ równań bezendu: W odpowiedziach mam, że są trzy rozwiązania a mi wychodzi tylko jedno |x−y|+x=6 x²+y=9 1⁰ x≥ i y≥0 x−y+x=6 ⇒−y=6−2x⇒y=2x−6 x²+2x−6=9 x²+2x−15=0 Δ=64 √Δ=8 x₁=−5∉D x₂=3∊D y=0 więc rozwiązaniem jest x=3 i y=0 2⁰ x≥0 i y<0 x₁=−1 ∉D x+y+x=6 ⇒y=6−2x x₂=3∊D x²−2x+6=9 y=0∉D x²−2x−3=0 Δ=16 √Δ=4 3⁰ x<0 i y<0 −x+y+x=6 y=6 od razu odrzucam bo∉D 4⁰ x<0 i y≥0 −x−y+x=6 ⇒−y=6 ⇒y=−6∉D gdzie robię błąd ? Może źle rozpisane warunki ?

PW: W 1° zakładasz x≥0 i y≥0. Wcale to nie znaczy, że x−y≥0, a tak rozumujesz. Dalej nie czytałem.

Piotr 10: Ten drugi warunek coś się nie zgadza, nie można zmienić znaku w środku bo to wartość dodatnia, ale zaraz to spróbuję sprawdzić

Saizou : ja bym zrobił tak I dla x≥y x−y+x=6 x²+y=9→y=9−x² 2x−y−6=0 2x−9+x²−6=0 x²+2x−15=0 (x+5)(x−3)=0 x₁=−5 x₂=3 y₁=−16 y₂=0 obydwa wyniki spełniają warunki II dla x<y −x+y+x=6 y=6 6=9−x² 3=x² x=√3 x=−√3 i x<y , czyli y=6 y=6 x=−√3 x=√3 i mamy nasze 4 rozwiązania

Piotr 10: Może zrób tak Ix−yI=6−x 6−x ≥0 x≤6 Ix−yI=6−x (..)²

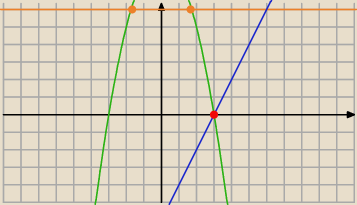
Mila: x²+y=9 y=−x²+9 1) |x−y|=x−y⇔x−y≥0⇔x≥y ⇔y≤x punkty poniżej prostej y=x Wtedy mamy układ równań x−y+x=6 y=−x²+9 2x−6=y i y=−x²+9 2x−6=−x²+9 x²+2x−15=0 x=−5 lub x=3 (sprawdź rachunki) x=−5, y=2*(−5)−6=−16 , −16<−5, para (−5,−16)∊D x=3, y=2*3−6=0 , 0<3 para (3,0)∊D 2) x−y<0⇔x<y⇔y>x Wtedy mamy układ −x+y+x=6 y=−x²+9 y=6 i y=−x²+9 6=−x²+9 x²−3=0 x=√3 lub x=−√3 x=√3, y=6 ⇒y>√3 para(√3,6)∊D para(−√3,6)∊D Odp. 4 rozwiązania: x=−5,y=−16 x=3,y=0 x=√3, y=6 x=−√3, y=6 Jednego rozwiązania nie widać.

bezendu: Czyli ja źle zrobiłem, już wiem gdzie mam błąd. Dziękuje bardzo za pomoc

Piotr 10: Mila a można zrobić te zadanie moim sposobem post 22:07 ?

Basia: C[Piotr 10 można tylko nie wiem czy potem będzie łatwo rozwiązać układ x² − 2xy + y² = 36 − 12x + x² x²+y = 9 y = 9−x² −2x(9−x²) + (9−x²)² −36 − 12x = 0 dać się da, ale nie tak łatwo chyba

Piotr 10: Ok, dzięki Basia

Mila: Ryzyko komplikacji przy podnoszeniu do kwadratu. Witaj Basia

Basia: Witaj Milu