Rozwiąż nierówność Paweł: Mam pytanko czy zadanie jest dobrze. Rozwiąż nierówność: (2x−5)(x²−4)(x³+8)≤0 Czy w takim wypadku mamy zbiór x−2<2;2,5>?

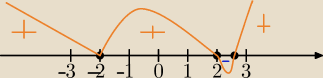Mila: (2x−5)(x²−4)(x³+8)≤0⇔

	5
2*(x−		)*(x−2)*(x+2)*(x+2)*(x2−2x+4)≤0 [x2−2x+4>0 dla x∊R]
	2

miejsca zerowe czynników liniowych:

	5
x=		, x=2, x=−2 pierwiastek podwójny
	2

odp.

	5
x∊<2,		>∪{−2}
	2

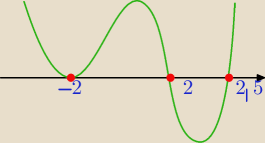bezendu: (2x−5)(x²−4)(x³+8)≤0 2(x−2,5)(x−2)(x+2)(x+2)(x²−2x+4)≤0 2(x−2,5)(x−2)(x+2)²(x²−2x+4)≤0 x∊<2,2,5>∪{−2}