Jednokładność Michal566: Witam. Mam takie zadanie : Okrąg F₁ o równaniu x² − 4x + y² − 4y = 0 jest obrazem w pewnej jednokładności okręgu F o równaniu x² + 2x + y² + 2y = 0. Wyznacz środek tej jednokładności oraz podaj jej skalę (rozpatrz dwa przypadki). Zacząłem : Obliczyłem równanie okręgu F = (x + 1)² + (y + 1)² = 2, więc r = √2 , S = (−1, −1) Równanie okręgu F₁ = (x − 2)² + (y − 2)² = 8 , więc r₁ = √8 = 2√2 , S = (2,2) Potem porównałem : r₁ = k * r 2√2 = k * √2 k = 2 Książka podaje w rozwiązaniu, że k = 2 v k = −2 Czy wcześniej powinienem skorzystać z wzoru na obraz odcinka |A^'B^'| = |k| * |AB| Korzystając z tego dostane te dwie skale, czy mogę uznać, że moje r jest długością SA gdzie A będzie dowolnym punktem na okręgu ? r₁ = |k| * r k = 2 v k = −2 Czy można tak to zrobić do tego momentu i teraz stanąłem jak dalej policzyć środek tej jednokładności ? Owe środki powinny wyjść (0,0) dla k = −2 lub (−4, −4) dla k = 2

Michal566: Ktoś ma pomysł

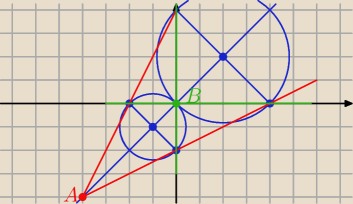
Bogdan: Rysunek wyjaśnia rozwiązanie A, B − środki jednokładności