Asymptoty funkcji Garth: Zbadaj, czy wykres podanej funkcji ma asymptoty poziome. Jesli tak, wyznacz ich rownania.

	x + 2		x2 − 3
f(x) =		dla |x| > 2 ∧		dla |x| ≤ 2
	1 − |x|		x2 − 16

Chcialem sie tylko upewnic − biorac pod uwage fakt, ze dla x ∊(−∞; −2)U(2; ∞) funkcja jest

	x + 2
okreslona wzorem		− wystarczy, ze policze granice w nieskonczonosci [lewo i
	1 − |x|

	x + 2
prawostronna] tej funkcji [		], a funkcja okreslona dla |x| ≤ 2 nie jest mi tu
	1 − |x|

potrzebna w przypadku okreslania asymptoty poziomej? Bo wyliczyc wyliczylem i wszystko sie zgadza z odpowiedziami.

asdf: Do badania granicy ukośnej (lepiej tak pisać, bo ukośna = pozioma, ale pozioma to juz nie ukośna) potrzebna jest dziedzina, jeżeli jej zbiór jest otwarty w przedziałach ±∞ to się ją

	f(x)
liczy. Pewnie łatwiej by Ci było gdybyś znał wyprowadzenie, dlaczego a = limx→±∞
	x

oraz dlaczego b = ... Wyprowadzić?

asdf: po 20 wrócę, ewentualnie pomogę.

Garth: W moim przypadku akurat dla funkcji okreslonej w |x| > 2 x ≠ 1 ∧ x ≠ −1, a wiec jest to juz wczesniej wykluczone. Natomiast nie jestem pewien, co rozumiesz przez "dlaczego a =

	f(x)		f(x)
limx→±∞		oraz dlaczego b = ...", czy tam mialo byc moze		? Wtedy bylo
	x		g(x)

by to dla mnie troche jasniejsze. Tez bede dopiero pozniej, wiec sie nie spieszy i dzieki za dotychczasowa pomoc.

asdf: y = ax + b "dlaczego a = lim (...) oraz dlaczego b = (...)" Chodzi mi o wyprowadzenie tych wzorów na as. ukośną.

Garth: To zadanko bylo w zadaniach do dzialu "asymptoty poziome", ktore jest przed dzialem "asymptoty ukosne" [z ktorym teraz sie zapoznalem, a jutro przerobie zadanka ze zbioru, ktory mam], takze teraz juz wiem, o co chodzi, ale autorom chyba chodzilo o zrobienie tego zadania bez wiedzi na temat asymptot ukosnych, takze ja tak tez je robilem. W ksiazce mialem tez dowod na to, ze: y = ax + b ⇔

	f(x)
⇔ limn→±∞[		] = a ∧ limn→±∞[f(x) − ax] = b, gdzie a, b sa granicami skonczonymi,
	x

wiec juz mniej wiecej wiem o co Ci chodzilo. Aczkolwiek, jesli chcialo by Ci sie wyprowadzac te wzory, to chetnie bym spojrzal tez na Twoj sposob [w mysl zasady od przybytku glowa nie boli ] − ale znowu nie nalegam, jezeli Ci sie nie chce. No i wielkie dzieki za pomoc.

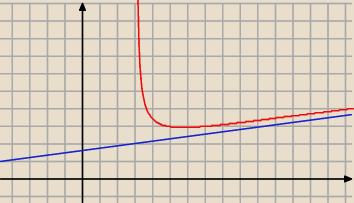
asdf: Ok, jest funkcja: f(x) oraz prosta h(x) = ax + b lim_x→∞ f(x) − h(x) = 0 (im dalej w prawo, tym różnica jest coraz mniejsza jak widać) lim_x→∞ f(x) − (ax + b) = 0 lim_x→∞ f(x) = ax + b // :x

	f(x)		b
limx→∞		= a +
	x		x

na pewno znasz wzór:

A		b
	= 0, tak tutaj		= 0
∞		x

	f(x)
limx→∞		= a
	x

	f(x)
a = limx→∞
	x

teraz b: lim_x→∞ f(x) = ax + b lim_x→∞ f(x) − ax = b b = lim_x→∞ [f(x) − ax] i tyle jeżeli a jest granicą zbieżną (jakaś wartość) to wtedy liczysz b, jeżeli b jest granicą zbieżną to masz asymptote ukośną: y = ax + b Dla wyjaśnienia: Granica pozioma to taki rodzaj granicy ukośnej, gdzie a = 0 nic więcej, dlatego jak będziesz liczyć zadania, to lepiej założyć, że szukasz ukośnej, a nie poziomej, bo jak napisalem wczesniej: ukosna = pozioma, ale pozioma to nie ukośna

Basia: asdf co to za bzdety znowu zadanie dobrze rozwiązane, a na końcu: ukośna = pozioma, ale pozioma to nie ukośna przecież to bzdura asymptota ukośna to prosta y=ax+b asymptota pozioma to prosta y = b pozioma jest szczególnym przypadkiem ukośnej ( a=0) równości tam nie ma żadnej jeżeli badasz czy istnieje ukośna to automatycznie wyliczysz poziomą jeżeli istnieje po prostu wyjdzie Ci to a=0, obliczysz b i gotowe wiem, że właśnie o to Ci chodziło, ale napisałeś coś strasznego

asdf: może inaczej: każdą poziomą można zaliczyć do ukośnej, ale każda ukośna to nie pozioma Wiadome o co chodzi...

asdf: z drugiej strony rozumiem Ciebie, bo jak to jedna osoba mi powiedziala: "dla matematyka znak równości to świętość"

Garth: Dzieki asdf i Basia. Troszke inaczej jest u mnie w podreczniku, ale wiadomo − sensu to nie zmienia.

Basia: jak już tak bardzo chcesz, żeby było formalnie, dokładnie i żeby to była prawda to musisz asdf użyć kwantyfikatorów ∀_a [ a jest pozioma ⇒ a jest ukośna]] ~∀_a [ a jest ukośna ⇒ a jest pozioma] ⇔ ∃_a [ a jest ukośna ∧ a nie jest pozioma]]