logarytmy zadanie: czy nierownosc log_x2<log_y2 jest prawdziwa dla x=0,13, y=0,97 ? czyli log_0,132<log_0,972 obie te funkcje sa malejace i maja wartosci ujemne ja zrobilem tak: jezeli 0,97>0,13 to log_0,132>log_0,972 wiec odp. nie dobrze?

PW: Obie są malejąca, ale to nie znaczy, że jedna z nich musi być stale większa od drugiej − z łatwością narysujesz przykłady − tak bez wzorów, same wykresy). To trzeba z definicji: log_0,132=x ⇔2=0,13^x log_0,972=y ⇔2=0,97^y 0,13^x=0,97^y Teraz walczysz, żeby pokazać relację miedzy x i y (która większa). Już na samym wstępie popełniasz błąd logiczny korzystając z tezy (zakładasz, że log_x2<log_y2, a oni pytają "czy").

pigor: ..., ja bym robił tak :

	log22		log22
(*)logx2< logy2 ⇔		<		⇔
	log2x		log2y

	1		1
⇔		<		⇔ (**)log2x > log2y, ale
	log2x		log2y

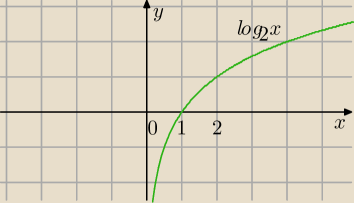
funkcja y=log₂x jest rosnąca, to znaczy x= 0,13 < 0,97=y ⇒ log₂x < log₂y , więc stąd, z (*) i (**) dana nierówność jest fałszywa (nie jest prawdziwa) . ...

zadanie: dziekuje

zadanie: mam problem z porownaniem x i y 0,13^x=0,97^y

pigor: ...,, no to np. tak : oczywiście x≠y≠0, a 0,13^x= 0,97^y ⇔ log0,13^x= log0,97^y ⇔

	x		log0,97
⇔ xlog0,13= ylog0,97 /: ylog0,13 ⇔ (*)		=		,
	y		log0,13

a ponieważ 0,97 > 0,13 ⇒ log0,97 > log0,13 , bo funkcja y= logx jest rosnąca, oraz log0,13< 0, więc nierówność log0,97 > log0,13 / : log0,13< 0 ⇔

	log0,97		x
⇔		< 1, zatem stąd i z (*)		< 1 ⇒x < y . ...
	log0,13		y

zadanie: dziekuje

zadanie: ale jezeli x<y to nierownosc jest prawdziwa a w odp. jest falszywa

pigor: ..., kurcze, a jakie było oryginalne (nie twoje) pytanie w zadaniu (a najlepiej dokładna treść zadania)

zadanie: tresc zadania jest taka jak na poczatku

Mila: Badam znak różnicy:

	1		1
logx2−logy2=		−		=
	log2x		logy2

	log2y−log2x		97   log2   37
=		=		>0⇔logx2>logy2
	log2x*logy		log2x*log2y

	97
log2		>0
	37

log₂ 0,37<0 log₂0,97<0

zadanie: dziekuje

Mila: Zmieniłam 0,13 na 0,37, ale to nie ma wpływu na wynik.