 Zadanie 2.
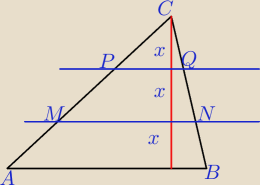
W trójkącie ostrokątnym poprowadzono dwie proste równoległe do podstawy, które podzieliły
wysokość trójkąta opuszczoną na tę podstawę na trzy odcinki równej długości. Oblicz stosunek
pól powstałych w wyniku tego podziału figur.
W odpowiedziach jest 1:3:5.
Zadanie 2.
W trójkącie ostrokątnym poprowadzono dwie proste równoległe do podstawy, które podzieliły
wysokość trójkąta opuszczoną na tę podstawę na trzy odcinki równej długości. Oblicz stosunek
pól powstałych w wyniku tego podziału figur.
W odpowiedziach jest 1:3:5.
| 1 | ||
PABC = | *24*3x = 36x | |
| 2 |
| 1 | 24 | |||
PQ = | *AB = | = 8 | ||
| 3 | 3 |
| 1 | ||
PPQC = | *8*x = 4x | |
| 2 |
| 2 | ||
MN = | *24 = 16 | |
| 3 |
| 1 | ||
PMNC = | *16*2x = 16x | |
| 2 |