równanie
Kostek:
Mam pewien problem mianowicie
rozwiąż równanie
|5−x|−|x+3|≥0
|x−5|−|x+3|≥0
1 (−
∞,−3)
−x+5+x+3≥0
0≥−8 fałsz
2) <−3,5)
−x+5−x−3≥0
−2x≥3
x≤1
3) <5,
∞)
x−5−x−3≥0
0≥8 fałsz
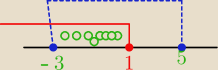
czyli biorę teraz część wspólną (−
∞,1> i <−3,5)
x∊<−3,1> a w odpowiedziach (−
∞,1>
16 wrz 19:10
Aga1.: 0≥−8 to prawda
16 wrz 19:12
Aga1.: A odp to 1)(−∞,−3)
2)<−3,1>
Suma tych cząstkowych odp. to
x∊(−∞,1>
16 wrz 19:14
Kostek: ok już wiem gdzie błąd dziękuje
16 wrz 19:15
Kostek: @Aga1 ale 0≥−8 większe tak ale równe ?
16 wrz 19:24
Aga1.: Kostek, miałeś logikę?
16 wrz 19:26
Kostek: nie
16 wrz 19:30
Kostek:
0≤9 to prawda ?
16 wrz 19:46
Mila:
Kostek , taki zapis:
9≥0 oznacza: 9 większe lub równe 0, spełniony jest jeden warunek,
zatem alternatywa jest prawdziwa.
Miałeś logikę w I klasie , zapomniałeś.
16 wrz 19:51
 Mam pewien problem mianowicie
rozwiąż równanie
|5−x|−|x+3|≥0
|x−5|−|x+3|≥0
1 (−∞,−3)
−x+5+x+3≥0
0≥−8 fałsz
2) <−3,5)
−x+5−x−3≥0
−2x≥3
x≤1
3) <5,∞)
x−5−x−3≥0
0≥8 fałsz
czyli biorę teraz część wspólną (−∞,1> i <−3,5)
x∊<−3,1> a w odpowiedziach (−∞,1>
Mam pewien problem mianowicie
rozwiąż równanie
|5−x|−|x+3|≥0
|x−5|−|x+3|≥0
1 (−∞,−3)
−x+5+x+3≥0
0≥−8 fałsz
2) <−3,5)
−x+5−x−3≥0
−2x≥3
x≤1
3) <5,∞)
x−5−x−3≥0
0≥8 fałsz
czyli biorę teraz część wspólną (−∞,1> i <−3,5)
x∊<−3,1> a w odpowiedziach (−∞,1>