Nierówności trygonometryczne Kamix: Bardzo proszę o sprawdzenie poniższego zadania: Naszkicuj wykres funkcji y=cosx, gdzie x∊<−2π,2π>. Na podstawie wykresu tej funkcji rozwiąż nierówność: a)cosx>−¹₂ w przedziale <−π,π> Mój wynik to: x∊(−^2π₃;^2π₃+2kπ), k∊ℂ b)cosx≥U{√2{2}} w przedziale <0,2π> Mój wynik to x∊<0;^π₄+2kπ>∪<^5π₃;2π+2kπ>, k∊ℂ c)|cosx|≤0, w przedziale <−2π,2π> Mój wynik to: x∊<−^3π₂;−^π₂+2kπ>∪<^π₂;^3π₂+2kπ>∪<−2π;−^3π₂+2kπ>∪<−u{π }{2};^π₂+2kπ>∪<^3π₂;2π+2kπ>, k∊ℂ d)2cosx+√3<0 w zbiorze ℛ Mój wynik to: x∊(−^7π₆;−^5π₆+2kπ), k∊ℂ Bardzo proszę o sprawdzenie, mi naprawdę długo zajęło wklepywanie tych wyników, a sprawdzenie poprawności dla Was ekspertów to kwestia chwili. DZIĘKUJĘ! ; )

PW: Tak patrzę wyrywkowo − na c) i nie mogę się nadziwić. Po co tak strasznie utrudniłeś sobie życie, gdy pytali o rozwiązanie nierówności w przedziale od −2π do 2π.

Kamix: Jestem taki człowiekiem, że gdy czegoś nie jestem pewny, to wole zapisać to w sposób taki, którego jestem pewny na 100%. A jak pozostałe przykłady? Czy są dobrze rozwiązane?

PW: Żadne nie jest dobrze rozwiązane. Na egzaminie ocenia się przede wszystkim, czy piszący zrozumiał polecenie i czy podał poprawną odpowiedź. Np. w c) pytali o rozwiązania z przedziału <−2π, 2π>. Podanie nieskończenie wielu rozwiązań będzie zakwalifikowane jako niezrozumienie polecenia. Kazali narysować − narysuj. Kazali odczytać z rysunku rozwiązania − odczytaj.

Mila:

	−2π		2π
a) x∊(		,		)
	3		3

	√2
b)cosx≥		i x∊<0,2π>
	2

	π		7π
x∊<0,		>∪<		,2π>
	4		4

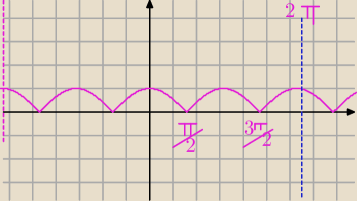
c))|cosx|≤0, w przedziale <−2π,2π> Ilustracja |cosx|≥0 z definicji wartości bezwzględnej, zatem interesują nas tylko miejsca zerowe

	π		−π		3π		−3π
x∊{		,		,		,		}
	2		2		2		2

Ostatni przykład za chwilę.

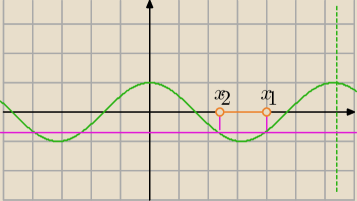
Mila: 2cosx+√3<0 w zbiorze ℛ⇔

	√3
cosx<−
	2

	√3		π		−π
cosx=		⇔x=		lub x=
	2		6		6

	−√3		7π		5π
cosx=		⇔x=		lub x=
	2		6		6

	√3
cosx<−
	2

	5π		7π
x∊(		+2kπ,		+2kπ)
	6		6

Sprawdzamy czy zgadzają się Twoje przedziały. k=−1

5π		7π		7π
	−2π=−		lub		−2π=−5π6
6		6		6

Zgadza się, ale popraw zapisy.

Kamix: Okey, bardzo, na prawdę bardzo dziękuję Mila, wiem, że było dużo pisania, ale teraz chociaż wiem, że potrafię rozwiązywać takie nierówności, bo nie miałem odpowiedzi.

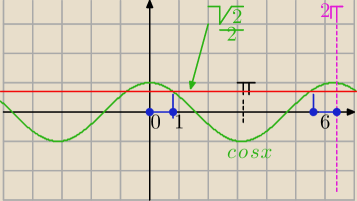
Mila: Jednak , tak jak radzi PW, rozwiązuj z wykresem. Ilustracja do (b)

	√2
cosx≥		w przedziale <0,2π>
	2

	π		7π
x∊<0,		>∪<		,2π>
	4		4