Geometria analityczna matma2013: Dany jest trójkąt ABC, o wierzchołkach A (−8,−2), B (4,−2), C (−8,3). Napisz równania prostych zawierających boki tego trójkąta i oblicz długość promienia okręgu opisanego na tym trójkącie.

Kostek: policz długości odcinków i pole ze wzoru Herona to nie jest trudne...

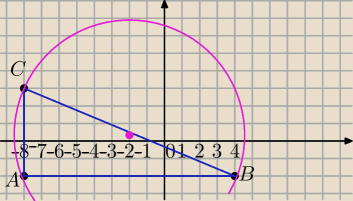
Mila: A (−8,−2), B (4,−2), C (−8,3) a) AB: y=−2 AC: x=−8 BC: y=ax+b −2=a*4+b 3=a*(−8)+b odejmuję stronami

	−5		5		5		−1
−5=12a⇔a=		, b=−2−4*(−		=−2+		=
	12		12		3		3

	−5		1
BC: y=		x−
	12		3

b) promień okręgu opisanego na Δ prostokątnym jest równy połowie przeciwprostokątnej.

	1
R=		|BC|
	2

|BC|=√12²+5² dokończ

5-latek: I teraz zobacz jak wazny jest rysunek Pozdrawiam Milu