wykaż
DukemNukem333:
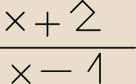
wykaż że funkcja f opisana wzorem f(x)= jest malejąca w przedziale od (− nieskończoności do 1)
15 wrz 22:43
Piotr 10: Założenie:
x−1≠0 ⋀ x
2>x
1 ⋀ x
2 − x
1>0
Teza:
f(x
1)>f(x
2)⇒f(x
1)−f(x
2)>0
Dowód:
| | x1+2 | | x2+2 | |
f(x1)−f(x2)= |
| − |
| =..... |
| | x1−1 | | x2−1 | |
Dokonaj przekształceń teraz
15 wrz 22:48
bezendu:
| x−1+3 | | 3 | |
| =1+ |
| D=R{1} |
| x−1 | | x−1 | |
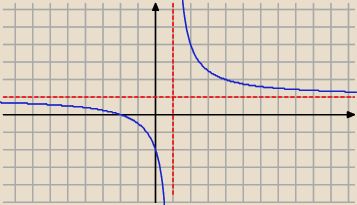
ale ta funkcja będzie ↘ x∊(−
∞,1)∪(1,
∞)
15 wrz 22:49
Piotr 10: I jeszcze w założeniu, że x∊(−∞;1)
15 wrz 22:49
Djuuuuuud: jak pomnoże np. x + 2 / x−1 licznik i mianownik przez x−1 to otrzymam x+2(x−1)?
15 wrz 22:54
Mila:
f(x) jest malejąca dla x∊D⇔Dla każdego x
1, x
2∊D z nierówności x
1<x
2 wynika nierówność
f(x
1)>f(x
2).
| | x+2 | |
f(x)= |
| i x<1⇔x−1<0 |
| | x−1 | |
dla x
1<x
2 mamy nierówność :
x1−x2<0
Wykażemy ,że f(x
1)>f(x
2)
Badamy znak różnicy:
| | x1+2 | | x2+2 | |
f(x1)−f(x2)= |
| − |
| = |
| | x1−1 | | x2−1 | |
| | (x1+2)*(x2−1)−((x2+2)*(x1−1)) | | 3(x2−x1) | |
= |
| = |
| >0 |
| | (x1−1)*(x2−1)) | | (x1−1)*(x2−1) | |
(licznik dodatni, mianownik dodatni)
⇔f(x
1)>f(x
2)
Cnw
15 wrz 23:01
Garth:
| | x + 2 | |
Jezeli chodzi o czysto algebraiczne rozwazania, to |
| * (x − 1) = x + 2, |
| | x − 1 | |
aczkolwiek nie wiem, jaki zwiazek mialo by to miec z powyzszym zadaniem, jesli takowego
poszukujesz. W przypadku tej funkcji nie mozesz sobie ot tak pomnozyc jej przez takie
wyrazenie.
15 wrz 23:03
Garth:
| | x + 2 | | x − 1 | |
Oj przepraszam, chyba chodzilo Ci o |
| * |
| ? |
| | x − 1 | | x − 1 | |
Wtedy otrzymasz wlasnie wyrazenie (x + 2)(x − 1), ale to bedzie zupelnie inna funkcja
[kwadratowa].
15 wrz 23:06
Djuuuuuud: dzięki
15 wrz 23:14
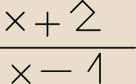 wykaż że funkcja f opisana wzorem f(x)= jest malejąca w przedziale od (− nieskończoności do 1)
wykaż że funkcja f opisana wzorem f(x)= jest malejąca w przedziale od (− nieskończoności do 1)
