Odwracanie macierzy
Ralph:
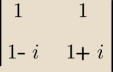
Jak odwrócić macierz w ciele liczb zespolonych? Albo jak wyglada macierz identycznosciowa liczb
zespolonych. Bo jak doklejam zwykla diagonalna z jedynkami na przekątnej to lipa.
Właśnie próbuje odwrócić powyższą macierz
15 wrz 22:42
Basia: tak samo jak w ciele R
W = 1*(1+i) − 1(1−i) = 1+i − 1 + i = 2i ≠0
więc jest odwracalna
A
−1 =
| 1+i | | (1+i)*i | | i+i2 | | −1+i | | 1 | | 1 | |
| = |
| = |
| = |
| = |
| − |
| i |
| 2i | | 2i2 | | −2 | | −2 | | 2 | | 2 | |
pozostałe przekształć tak samo
| | | |
albo metodą Gausa z dopisaną macierzą | |
| | |
15 wrz 22:50
Ralph: no i mi sie nie zgadza bo w prawym górnym rogu macierzy odwróconej wychodzi 1/2 + (1/2)i , a
powinno byc (1/2)i samo
15 wrz 23:44
Ralph: a metoda Gausa wogole porazka bo wtedy wychodzi:
| (1+i)/(2i) −1/(2i) |
| (−1+i)/(2i) 1/(2i) |
i zdaje sie ze rachunki są wykonane dobrze:(
15 wrz 23:47
Basia:
mogłam się pomylić; policz metodą Gausa
15 wrz 23:52
Basia: zapomniałam ją transponować
i teraz dzielimy każdy wyraz przez 2i
| | 1+i | | i(1+i) | | 1 | | 1 | |
x11 = |
| = |
| = |
| − |
| i |
| | 2i | | −2 | | 2 | | 2 | |
| | −1 | | −i | | i | |
x12 = |
| = |
| = |
| |
| | 2i | | −2 | | 2 | |
| | −1+i | | −i−1 | | 1 | | 1 | |
x21 = |
| = |
| = |
| + |
| i |
| | 2i | | −2 | | 2 | | 2 | |
ale jeszcze posprawdzaj
16 wrz 00:07
Ralph: sprawdzilem, wszystko się zgadza. Myśle, że jednak krócej jest metodą Gausa(może akurat na tym
przykładzie). Bardzo dziękuje !
16 wrz 20:08
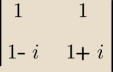 Jak odwrócić macierz w ciele liczb zespolonych? Albo jak wyglada macierz identycznosciowa liczb
zespolonych. Bo jak doklejam zwykla diagonalna z jedynkami na przekątnej to lipa.
Właśnie próbuje odwrócić powyższą macierz
Jak odwrócić macierz w ciele liczb zespolonych? Albo jak wyglada macierz identycznosciowa liczb
zespolonych. Bo jak doklejam zwykla diagonalna z jedynkami na przekątnej to lipa.
Właśnie próbuje odwrócić powyższą macierz