pole czworokata Madzik: Przekątne równoległoboku o polu równym 16√2 cm² przecinają się pod kątem, którego sinus wynosi ^2√2₃. Jedna z przekątnych tego równoległoboku jest trzykrotnie dłuższa od drugiej. a) Uzasadnij, ze krótsze boki tego równoległoboku są prostopadłe do jednej z przekątnych. b) Oblicz obwód tego równoległoboku.

Madzik: pomoże ktoś?

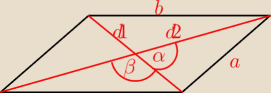
ZeroOsiem: Można wykorzystać wzór:

	d1*d2
P=		*sinα
	2

Wiemy, że d₂=3*d₁, a sinα=^2√2₃

	3*(d1)2
P=		*sinα
	2

Po przekształceniach wyznaczymy d₁=4 i d₂=3*d₁=12 Żeby obliczyć boki wykorzystamy tw. cosinusów cosα=√1−sinα²=¹₃

	d1		d2		d1		d2
a2=(		)2+(		)2−2*		*		*cosα
	2		2		2		2

a=4√2 β=180−α ale cos(180−α)=−cosα

	1
cosβ=−
	3

	d1		d2		d1		d2
b2=(		)2+(		)2−2*		*		*cosβ
	2		2		2		2

b=4√3 a)Sprwadź z tw. Pitagorsa. Jeśli zachodzi to jest bok prostopadły do przekątnej a²+(d₁)²=b² b)Ob=2*a+2*b

Madzik: A skąd to sie wzięło, ta potega? P=^3*(d1)2₂*sinα

ZeroOsiem: d₂=3*d₁ więc d₂*d₁=3d₁*d₁=3(d₁)²

Madzik: dobra okej, zrozumiałam, ale dalej i tak nie ma szans, nie miałam jeszcze twierdzenia cosinusów; sin, cos i tg, jako tako miałam, ale do twierdzeń nie doszliśmy jeszcze