geometria zadanie: 3. Czy w podanym zbiorze trójkatów istnieja trójkaty o dowolnie duzym obwodzie a) zbiór trójkatów o iloczynie długosci boków równym 1 ; b) zbiór trójkatów opisanych na okregu o promieniu 1 ; c) zbiór trójkatów wpisanych w okrag o promieniu 1 ; d) zbiór trójkatów o polu 1 ? Odp.: a. T b. T c. N d. T a) tak, bo mozna dowolnie dobierac dlugosci bokow b) tak samo jak w a) c) tego nie wiem jak wytlumaczyc d) tak samo jak w a) 4. Czy w podanym zbiorze trójkatów istnieja trójkaty o dowolnie duzym polu a) zbiór trójkatów o iloczynie długosci boków równym 1 ; b) zbiór trójkatów opisanych na okregu o promieniu 1 ; c) zbiór trójkatów o obwodzie 1 ; d) zbiór trójkatów wpisanych w okrag o promieniu 1 ? Odp.: a. N b. T c. N d. N nie wiem czy sa to dobre argumenty dlatego poprosilbym o sprawdzenie

zadanie: ?

Mila: Trójkąty wpisane w okrąg o promieniu 1, mają ograniczone obwody i pole. Wykonaj rysunek.

zadanie:

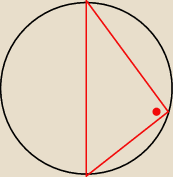
zadanie: bo dlugosci bokow i wysokosci musza znajdowac sie we wnetrzu okregu a promien moze byc dowolny

zadanie: 4 b) tak, bo mozna dowolnie dobierac dlugosci bokow 4 a) i c) jakie jest tu ograniczenie i czym sie rozni od tego z zadania 3 w sensie obwod a pole?

Mila: 3) Właśnie promień nie jest dowolny, jest równy 1, stąd ograniczenie dla długości boków. Trójkąt o polu 1.

	1
P=		ab*sinα=1
	2

	2
ab=		przy ustalonym α, możesz dobierać a i b, c będzie odpowiednio wyznaczone .
	sinα

4) a) zbiór trójkątów o iloczynie długości boków równym 1 ;

	1
P=		a*b*sinα
	2

c) zbiór trójkątów o obwodzie 1 ;

	1
P=		a*b*sinα<1
	2

a<1, b<1, c<1 a+b+c=1

zadanie: dziekuje

Mila: