Planimetria; twierdzenie sinusów
Ola: Jedna z przyprostokątnych trójkąta prostokątnego ma długość a i jest 4 razy krótsza od
przeciwprostokątnej. Oblicz długości promieni okręgów opisanych na trójkątach otrzymanych z
podziału danego trójkąta środkową poprowadzoną z wierzchołka kąta prostego. Z góry dziękuję
15 wrz 13:34
Bogdan:
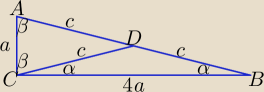
β = 90
o − α, sinβ = cosα
2c = ...
| | a | | 4a | |
sinα = |
| , cosα = |
| |
| | 2c | | 2c | |
Korzystając z tw. sinusów:
| | c | |
R1 − długość promienia okręgu opisanego na trójkącie CBD: R1 = |
| |
| | 2sina | |
R
2 − długość promienia okręgu opisanego na trójkącie CDA: R
2 = ...
15 wrz 14:10
pigor: ..., łatwo wykazać, że długość środkowej =
12*4a= 2a ,
wtedy np.
| | a | | 2a | | 2 | |
sinα= |
| = 14 i sinβ= |
| = |
| , więc z tw. sinusów : |
| | 4a | | √17a | | √17 | |
| | 2a | | 2a | |
2R1= |
| i 2R2= |
| odpowiednio ⇒ |
| | sinα | | sinβ | |
⇒
R1= 4a i
R2= 12√17a , o ile gdzieś nie rąbnąłem się . ...
15 wrz 14:14
Bogdan:
Moje rozwiązanie (teraz zauważyłem) dotyczy sytuacji, w której jedna z przyprostokątnych
jest 4 razy większa od drugiej. W zadaniu podanym przez
Olę przeciwprostokątna
jest 4 razy dłuższa od jednej z przyprostokątnych, a więc rozwiązanie, które przedstawiłem
nie dotyczy zadania
Oli
15 wrz 14:27
ZeroOsiem: Druga przyprostokątna z tw. Pitagorasa =
√15a
Dodatkowo policz cosα i cosβ, sinα i sinβ pozostałych kątów oraz pole swojego trójkąta.
cosα=
14, cosβ=
√154
sinα=
√154, sinβ=
14
P=
√15a24
Środkową oznaczmy jako x.
Wyznaczymy ją z tw.cosinusów dla dowolnego trójkąta z tych już podzielonych:
x
2=4a
2+a
2−2*2a*a*cosα =4a
2
x=2a
Z Tw. sinusów wyznaczymy promienie okręgów opisanych na trójkątach
1 trójkąt:
| | x | | 2a | | 4a | |
R= |
| = |
| }= |
| |
| | 2sinα | | √152 | | √15 | |
2 trójkąt
15 wrz 14:30
pigor: ...no tak czułem ... , okazuje się, że . ...
"nie znam" tw. Pitagorasa
15 wrz 14:32
Bogdan:
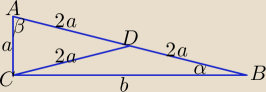
b = a
√15
| | a | | 1 | | b | | √15 | |
sinα = |
| = |
| , sinβ = cosα = |
| = |
| |
| | 4a | | 4 | | 4a | | 4 | |
| | 2a | |
R1 − długość promienia okręgu opisanego na trójkącie CBD: R1 = |
| = 4a |
| | 2sinα | |
| | 2a | | 4a | |
R2 − długość promienia okręgu opisanego na trójkącie CDA: R2 = |
| = |
| |
| | 2sinβ | | √15 | |
15 wrz 14:40
Bogdan:
Środkowa w trójkącie prostokątnym poprowadzona na przeciwprostokątną jest jednocześnie
promieniem okręgu opisanego na tym trójkącie, czyli przyjmując oznaczenie ZeroOsiem
otrzymujemy x = 2a
15 wrz 14:42