Funkcja
bezendu:
Dana jest funkcja f(x)=x
2. Rozważmy trójkąt o wierzchołkach (0,0), (a,f(a)) i (−a,f(−a)) gdzie
a∊R−{0}
Uzasadnij, że pole tego trójkąta jest równe P=a
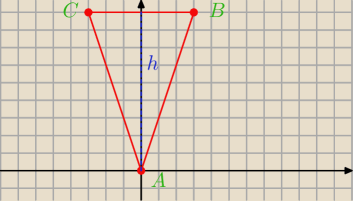
3. Wykonaj ilustracje graficzną w przypadku a=3
|CB|=6
|AB|=p{

3−0)
2+(9−0)
2=3
√10
h=9
ok ?
14 wrz 22:01
bezendu: |AB|=
√(3−0)2+(9−0)2=3
√10 nie wiem czemu wyskoczyło

14 wrz 22:03
Saizou : no to mamy punkty
A=(0:0)
B=(a:a
2)
C=(−a:(−a)
2)=(−a:a
2)
i ze wzoru na pole trójkąta o danych wierzchołkach mamy
| | 1 | |
P= |
| l(a−0)(a2−0)−(a2−0)(−a−0)l= |
| | 2 | |
| | 1 | | 1 | |
= |
| la3+a3l= |
| l2a3l=la3l |
| | 2 | | 2 | |
no i dla a=3
P=l3
3l=l27l=27
14 wrz 22:08
Basia:
nie trzeba tak komplikować;
przecież widać, że (D − punkt przecięcia podstawy z OY)
| | 1 | |
PABC = 2*PABD = 2* |
| *DB*DA = DB*DA = a2*|a| = |a3| |
| | 2 | |
dla a>0 to jest oczywiście P = a
3
14 wrz 22:12
Saizou : to była pierwsza myśl

14 wrz 22:14
 Dana jest funkcja f(x)=x2. Rozważmy trójkąt o wierzchołkach (0,0), (a,f(a)) i (−a,f(−a)) gdzie
a∊R−{0}
Uzasadnij, że pole tego trójkąta jest równe P=a3. Wykonaj ilustracje graficzną w przypadku a=3
|CB|=6
|AB|=p{
Dana jest funkcja f(x)=x2. Rozważmy trójkąt o wierzchołkach (0,0), (a,f(a)) i (−a,f(−a)) gdzie
a∊R−{0}
Uzasadnij, że pole tego trójkąta jest równe P=a3. Wykonaj ilustracje graficzną w przypadku a=3
|CB|=6
|AB|=p{ 3−0)2+(9−0)2=3√10
h=9
3−0)2+(9−0)2=3√10
h=9

