Logarytm bezendu: Wyznacz dziedzinę funkcji f(x)=log_x²−3(x³+4x²−x−4) i zapisz ją w postaci sumy przedziałów liczbowych x²−3>0 x³+4x²−x−4>0 (x−√3)(x+√3) x²(x+4)−(x+4)>0 (x+4)(x−1)(x+1)>0 x∊(−∞,−√3)∪(√3,∞)∪(−4,−1)∪(1,∞) Jednak w odpowiedziach mam inną odpowiedź

Antek: Ale tez podstawa ≠1 czyli x²−3≠1

Saizou : x²−3>0 i x²−3≠1 i x³+4x²−x−4>0 x²−3>0 x²>3 x>√3 lub x<−√3 x∊(−∞:−√3) ∪(√3:+∞) x²−3≠1 x²≠4 x≠2 lub x≠−2 x³+4x²−x−4>0 x²(x+4)−1(x+4)>0 (x+4)(x−1)(x+1)>0 x=−4 x=1 x=−1 x∊(−4:−1)∪(1:+∞) zatem x∊(−∞:−√3∪(√3:+∞) \{−2:2} jak się nie kopnąłem

bezendu: Dziękuje zapomniałem właśnie jednego warunku

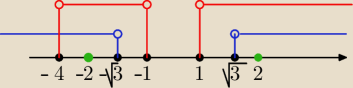
Basia: podstawa ≠ 1 czyli jeszcze x²−3 ≠ 1 x²−4≠0 (x−2)(x+2)≠0 x≠ −2 i x≠2 poza tym wszystkie warunki mają być spełnione x∊[ [(−∞;−√3)∪(√3;+∞)] ∩ [(−4,−1)∪(1,∞)] ] \ {−2;2} x∊(−4;−2)∪(−2;−√3)∪(√3;2)∪(2;+∞)

Basia: kopnąłeś się Saizou ma być: x²−3>0 i x²−3≠1 i x³+4x²−x−4>0 i czyli iloczyn zbiorów

bezendu: Basia w odpowiedziach jest tak jak podałaś Czyli biorę część wspólną tych warunków i zapisuje w potem jako sumy zbiorów ?

Saizou : Basiu coś ostatnio jestem zbyt roztrzepany

Basia: tak bezendu roztrzepany = zakochany Saizou ? bywa, bywa

Saizou : chciałaś napisać chyba roztrzepany ≠ zakochany

Basia: ależ to nic złego, przeciwnie

Saizou : bądź co bądź, nie jestem zakochany, no może w kulturze Japonii, ale to inna bajka

bezendu: Ok dziękuje zapamiętam

informatyk: bezendu umie przewidywać matury z polaka

Basia: Dobranoc wszystkim. Kolorowych snów.

Basia: Mam jeszcze trochę roboty, więc już chyba na dzisiaj koniec

bezendu: Dobranoc @informatyk wszyscy w domu zdrowi ?

Saizou : Basiu Oyasumi i miłych snów