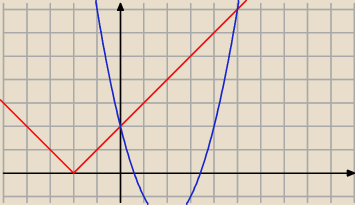
Proszę o pomoc . Bo czekam Martyna 0: Równania sprowadzalne do równań kwadratowych. Rozwiąż Równanie b) x do kwadratu −4x +2 =|x+2|

PW: Martyna, ja już czekam 45 lat ... x²−4x+2 = (x−2)²−2 = (x−2−√2)(x−2+√2) Lewą stronę rozkładamy na czynniki, żeby korzystając z własności funkcji kwadratowej ustalić, gdzie przyjmuje wartości dodatnie lub zero, a gdzie ujemne. Tam, gdzie przyjmuje wartości ujemne − rozwiazań na pewno nie będzie, bo prawa strona jest nieujemna.

Basia: x² − 4x + 2 = |x+2| x≥−2 i x² − 4x + 2 = x+2 lub x<−2 i x² − 4x + 2 = −x −2 x≥−2 i x² − 5x = 0 lub x<−2 i x² − 3x + 4 = 0 x≥2 i x(x−5) = 0 ⇔ x=0 lub x=5 x< −2 Δ = 9 − 4*1*4 < 0 nie ma rozwiązania Odp: x=0 lub x=5

pigor: ..., np. tak : x²−4x+2= |x+2| ⇔ (x+2<0 i x²−4x+2= −x−2) lub (x+2 ≥0 i x²−4x+2= x+2) ⇔ ⇔ (x< −2 i x²−3x+4= 0) lub (x ≥ −2 i x²−5x= 0) ⇔ ⇔ (x< −2 i x∊∅) lub (x ≥ −2 i x(x−5)= 0) ⇔ ⇔ x ≥ −2 i (x=0 lub x=5) ⇔ x=0 lub x=5 ⇔ x∊{0,5}.. ...

bezendu: ''Bo czekam ?''

PW: Tak od razu "kawa na ławę" wszystko ... A ja się chciałem z Martyną podrażnić.

PW: Martyno, a tak poważniej: wszyscy na ogół rzucają się szukać gdzie jest rozwiązanie. W niektórych wypadkach dobrze jest ustalić, gdzie na pewno rozwiązań nie ma. Potem robi się wszystko jaśniejsze. Ten przykład może nie był najlepszy (chociaż, gdy spojrzeć na rysunek Basi, to coś w tym jest).