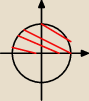
 Oblicz ∫∫D ex2+y2 dxdy, gdzie D: x2+y2≤1 i y≥0 aha x2+y2 to potęga e
x=rcosφ
y=rsinφ
obszar
0≤r≤1
0≤φ≤π
czyli
∫01 dr ∫0π er2cos2φ+r2sin2φ * rdφ aa r2cos2φ+r2sin2φ to potęga e
czyli po uproszczeniu wzór wyjdzie taki
∫01 dr ∫0π er2 * rdφ
∫0π er2 * rdφ = er2 * r*φ |0π = πrer2
∫01 πrer2 dr
t=r2
dt=2rdr
dt/2=rdr
∫01 πet dt/2 = 1/2 π ∫ et dt =1/2π er2 |01
1/2πe1 = 1/2πe
tak to ma wyglądać?
Oblicz ∫∫D ex2+y2 dxdy, gdzie D: x2+y2≤1 i y≥0 aha x2+y2 to potęga e
x=rcosφ
y=rsinφ
obszar
0≤r≤1
0≤φ≤π
czyli
∫01 dr ∫0π er2cos2φ+r2sin2φ * rdφ aa r2cos2φ+r2sin2φ to potęga e
czyli po uproszczeniu wzór wyjdzie taki
∫01 dr ∫0π er2 * rdφ
∫0π er2 * rdφ = er2 * r*φ |0π = πrer2
∫01 πrer2 dr
t=r2
dt=2rdr
dt/2=rdr
∫01 πet dt/2 = 1/2 π ∫ et dt =1/2π er2 |01
1/2πe1 = 1/2πe
tak to ma wyglądać?
| 1 | π | |||
∬D ex2+y2 dxdy = ∫01 rer2dr ∫0π dφ = π* | ∫01 eudu = | (e−1). | ||
| 2 | 2 |