 Nie wiem czy dobrze rozumiem...
Mam obliczyć całkę ∬D (x+2y) dxdy którego obszarem ograniczonym jest trójkąt o bokach
A(0,0);B(2,2);C(2.4).
Obliczyłam proste AC i AB
AC ogranicza z góry i równa jest y=2x
AB ogranicza z dołu i wynosi x
Moje pytanie czy mogę przyjąć takie obszary całkowania. Podzieliłam trójkąt na 2 obszary D1 i
D2
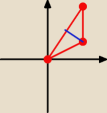
Linia niebieska na rysunku. ten bliżej punktu 0,0 to dajmy na to D1
I tak obszar całkowania D1
0≤x≤2
x≤y≤2x
a obszar całkowania D2 tu nie jestem pewna czy mogę tak przyjąć
0≤x≤2
2≤y≤4
Proszę o pomoc, czy może to tak wyglądać czy ten obszar całkowania D2 zmienić.
Nie wiem czy dobrze rozumiem...
Mam obliczyć całkę ∬D (x+2y) dxdy którego obszarem ograniczonym jest trójkąt o bokach
A(0,0);B(2,2);C(2.4).
Obliczyłam proste AC i AB
AC ogranicza z góry i równa jest y=2x
AB ogranicza z dołu i wynosi x
Moje pytanie czy mogę przyjąć takie obszary całkowania. Podzieliłam trójkąt na 2 obszary D1 i
D2
Linia niebieska na rysunku. ten bliżej punktu 0,0 to dajmy na to D1
I tak obszar całkowania D1
0≤x≤2
x≤y≤2x
a obszar całkowania D2 tu nie jestem pewna czy mogę tak przyjąć
0≤x≤2
2≤y≤4
Proszę o pomoc, czy może to tak wyglądać czy ten obszar całkowania D2 zmienić.
| 4 | 4 | 32 | ||||
J = 0∫24x2dx = | x3 0|2 = | (8−0) = | ||||
| 3 | 3 | 3 |
