granica wajs: Proszę o pomoc, jak to zrobić Oblicz granicę funcji lim 1 3 x→1 −−−− − −−−−− 1−x 1−x³ W odpowiedziach mam −1

Mila:

	1		3
limx→1[		−		]=
	1−x		(1−x)*(1+x+x2)

	1+x+x2−3
=limx→1		=
	(1−x)*(1+x+x2)

	x2+x−2
=limx→1		=
	(1−x)*(1+x+x2)

	(x−1)*(x+2)
=limx→1		=
	(1−x)*(1+x+x2)

	(−1)*(x+2)		−(1+2)
=limx→1		=		=−1
	(1+x+x2)		1+1+1

Mila: ?

wajs: dobrze dobrze , dziękuje Jeszcze jeden problem :

	1
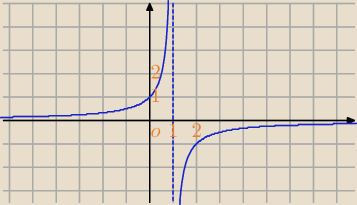
limx→1+
	1−x

Mila:

	1		1
limx→1+		=[		]=−∞
	1−x		0−

	1		1
limx→1−		=[		]=∞
	1−x		0+

wajs: Dziękuje