układ rownan
Ralph:
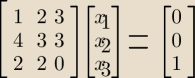
Znajdź wszystkie rozwiązania układu nad Z
5 .
Dodam, ze powinno ich być 5, a to wynika z tego ze jestesmy własnie w ciele Z
5 o ile sie nie
myle.
Jest jakis lepszy sposob wypisania macierzy niz rysowanie

13 wrz 17:10
Ralph: Dodam jeszcze ze B nie jest odwracalna
13 wrz 17:32
Ralph: tzn ta macierz po samej lewej..
13 wrz 17:32
Basia:
a dlaczego nie ?
W = 1*3*0 + 2*3*2 + 3*4*2 − [ 3*3*2 + 3*2*1 + 0*2*4 ] =
12+24 − [18+6] = 36 − 24 = 12
13 wrz 17:43
Ralph:
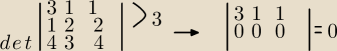
więc B nie jest odwr. w M
3(Z
5). Dlatego....Chyba ze odwraca sie normalnie a nie w ciele Z
5

13 wrz 17:51
Basia: niestety to nie tex; nx2 jeszcze się da (wykorzystując symbol Newton
ale więcej niż dwóch wierszy raczej nie uzyskamy
co u Ciebie oznacza Z
5 ? bo to za każdym razem co innego
13 wrz 18:00
Basia: 2xn oczywiście
13 wrz 18:00
Ralph: ta macierz jest o współczynnikach w Z5. I mam znależć wszystkie roziwazania układu nad Z5.
Z5 oznacza ciało
13 wrz 18:03
Basia: jakie ciało ? o to pytam
13 wrz 18:12
Ralph:
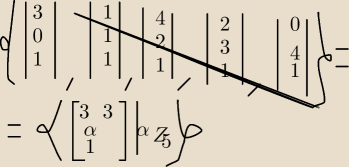
pomiedzy trójkami tam jest + w w kółeczku, i dalej α∊Z
5. To jest rozwiązanie ....ale jak do
tego dojsc:(
13 wrz 18:17
Ralph: przepraszam za tą kreske przekr. ale jak rysowalem jej nie bylo... Ciało liczb całkowitych...
13 wrz 18:18
Basia: modulo 5 zapewne ?
jeżeli tak to pomyślę, może sobie przypomnę jak to się robiło
13 wrz 18:45
Ralph: jeszcze jeden bład....na samej górze podalem zla macierz....eh...Dobra macierz jest tam gdzie
policzylem wyznacznik
13 wrz 18:50
Ralph: tak chodzi o modulo 5 własnie
13 wrz 19:02
Basia: no tak, teraz rozumiem wreszcie dlaczego ona nie jest odwracalna
jej wyznacznik = 5 =mod50
13 wrz 19:03
Ralph: nie wiem w sumie, czy mozna narzucic modulo dopiero po obliczeniu bo pare razy kiedys w ten
sposob wyszło mi zle. Tak czy siak jest nieodwracalna i pokazalem to wyzej mnorzac pierwszy
wiersz przez 3 i dodajac do drugiego wiersza. Na to modulo i wychodzi cały zerowy wiersz, więc
det = 0. W sumie juz doszedłem o co chodzi. Dokleiłem wektor [0 0 1] do Macierzy i na całości
zrobilem elminacje gausa mod 5, az doprowadzilem do postaci całkowicie zredukowanej i wyszło
ze x1= −2x2+3, x2 ∊Z5, x3 = 1. A 5 wektorów tego rozwiazania powyzej powstało z podstawiania
za x2 kolejno 0, 1, 2 , 3, 4 bo od 5 sie znowu rozw powtarza gdyz 5 mod 5 = 0. nie wiem tylko
jeszcze skad sie bierze ta prawa strona równosci rozwiązania...
13 wrz 20:26
Basia: to powinno być: 3+α*3
3+0*3 = 3
3+1*3=6 =51
3+2*3 = 954
3+3*3 = 1252
3+4*3 = 1550
czyli rozwiązaniem jest zbiór wektorów (pionowych) takich, że
[ 3 + α*3; α; 1 ] gdzie α∊Z5
14 wrz 00:18
Ralph: aha, ja poprostu mialem −2*α bo nie narzucilem modulo 5.
wszystko juz rozumiem. Dziękuje!

14 wrz 00:35
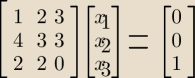 Znajdź wszystkie rozwiązania układu nad Z5 .
Dodam, ze powinno ich być 5, a to wynika z tego ze jestesmy własnie w ciele Z5 o ile sie nie
myle.
Jest jakis lepszy sposob wypisania macierzy niz rysowanie
Znajdź wszystkie rozwiązania układu nad Z5 .
Dodam, ze powinno ich być 5, a to wynika z tego ze jestesmy własnie w ciele Z5 o ile sie nie
myle.
Jest jakis lepszy sposob wypisania macierzy niz rysowanie
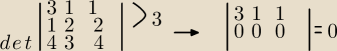 więc B nie jest odwr. w M3(Z5). Dlatego....Chyba ze odwraca sie normalnie a nie w ciele Z5
więc B nie jest odwr. w M3(Z5). Dlatego....Chyba ze odwraca sie normalnie a nie w ciele Z5

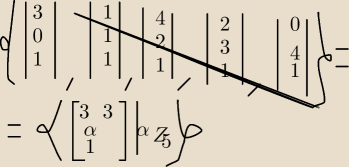 pomiedzy trójkami tam jest + w w kółeczku, i dalej α∊Z5. To jest rozwiązanie ....ale jak do
tego dojsc:(
pomiedzy trójkami tam jest + w w kółeczku, i dalej α∊Z5. To jest rozwiązanie ....ale jak do
tego dojsc:(
