obliczyć całki podwójne Janek: _D∫∫ y dxdy D: x²+y² = R² Nie mam pojęcia w jaki sposób to rozwiązać

Basia: przejdź na współrzędne biegunowe

Janek: a jakiś inny sposób? Bo w podręczniku to jest w innym dziale, nie w dziale ze wspołrzędnymi biegunowymi

Janek: po za tym współ. biegunowe sprawiają mi mały problem

Janek: tzn. ten problem jest dosyć spory

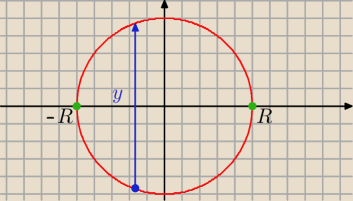
Trivial: Jeżeli boisz się współrzędnych biegunowych (naprawdę upraszczają sprawę), to znajdź granice w układzie (x,y) i całkuj "na chama". Górna część okręgu wyraża się równaniem y = +√R2 − x2. Dolna część: y = −√R2 − x2 ∬D y dxdy = ∫−RR dx ∫−√R2 − x2√R2 − x2 y dy Powodzenia w liczeniu.

Basia: D to koło S(0,0) r=R możesz tak: P = _−R∫^Rdx ₀∫^√R2−x2ydy + ₋R∫^Rdx _{−√R²−x²}∫⁰ydy ale to dużo trudniej

Janek: Ok dzięki, spróbuje z tego wyliczyć, jeżeli to mi się nie uda spróbuje opanować współrzędne biegunowe

Janek: Czy o to chodzi ? x=ςcosφ ; 0≤φ ≤2π y=ςsinφ ; 0≤ς≤R J=ς J=₀∫^2π dφ ₀∫^R ς (ςsinφ) dς

Basia: właśnie o to

Janek: J₁=₀∫^2π dφ=φ₀|^2π=2π

	ς3
J2=0∫R ς2 sinφ dς=		sinφ0|R dobrze ?
	3

Trivial: J = ∬_D y dxdy = ∬_G r²sinφ drdφ = ∫₀^R r²dr ∫₀^2π sinφdφ Jako, że granice są od siebie zupełnie niezależne, rozbijamy na iloczyn całek: J = ∫₀^R r²dr * ∫₀^2π sinφdφ = ¹₃R³ * [−cos(2π) + cos(0)] = 0.

Janek: Chyba rozumiem, dzięki

Trivial: W sumie bez przejścia na zmienne biegunowe też nie jest za ciężko: ∬D y dxdy = ∫−RR dx ∫{−√R2−x2{√R2−x2 ydy = ∫−RR 12[y2]y=−√R2−x2y=√R2−x2 dx = ∫−RR 12[R2−x2 − (R2−x2)] dx = 0

Janek: Po tym jak napisałeś,że to dość trudne,a potem Basia to potwierdziła uznałem,że lepiej jak spróbuje współ. biegunowymi i nawet nie zrobiłem ta pierwszą metodą. Chociaż jak to rozpisałeś to faktycznie nie wygląda strasznie