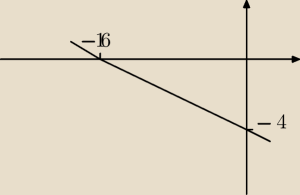
 Znaleźć środek ciężkości jednorodnej płytki ograniczonej liniami y=x2−16 , y=0
Czy chodzi w tym zadaniu o to:
Znaleźć środek ciężkości jednorodnej płytki ograniczonej liniami y=x2−16 , y=0
Czy chodzi w tym zadaniu o to:
|
| |||||||||||||||
∫∫dxdy=∫dx*∫dy=x| | * y| | = (−16)*(−4) = 64  | ||||||||||||||
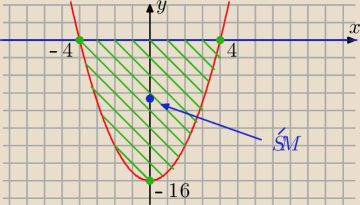 Raczej nie...
Skąd wziął się Twój rysunek? Trzeba narysować wykresy y = x2 − 16 oraz y = 0.
Z symetrii względem osi y oraz z tego, że płytka ma jednorodny rozkład masy oczywiste jest, że:
xŚM = 0
Raczej nie...
Skąd wziął się Twój rysunek? Trzeba narysować wykresy y = x2 − 16 oraz y = 0.
Z symetrii względem osi y oraz z tego, że płytka ma jednorodny rozkład masy oczywiste jest, że:
xŚM = 0
| M | ||
Szukamy środka masy na osi y. Wprowadzamy gęstość powierzchniową σ = | ||
| S |
| 1 | 1 | σ | ||||
yŚM = | ∬M ydm = | ∬S σy dxdy = | ∫−44 dx ∫0x2−16 ydy | |||
| M | M | M |
| 1 | (x2−16)2 | 213 | ||||
= | ∫−44 − | dx = ... = − | ||||
| S | 2 | 15*S |
| 28 | ||
S =∬S dxdy = ∫−44 dx ∫0x2−16 dy = ∫−44 (16 − x2)dx = ... = | ||
| 3 |
| 213 | 3 | 25 | 32 | |||||
yŚM = − | * | = − | = − | . | ||||
| 15 | 28 | 5 | 5 |