Geometria analityczna Guma polimer naturalny modyfik: Dane są punkty K = (−1, −20) i L = (3, 4). Znajdź na osi x taki punkt A, aby trójkąt kal był prostokątny. Mi za każdym razem wychodzi (−4, 0) i drugi przypadek (9, 0) a powinno wyjść A = ( 1 − 2 √3, 0) lub A = ( 1 + 2 √3, 0) O co chodzi Proszę pomóżcie.

sushi_ gg6397228: zapisz swoje obliczenia

Guma polimer naturalny modyfik: ok

Guma polimer naturalny modyfik: Liczyłem prostą [KL] k{−2= − 1a +b &4= 3a + b a=³₂ y=³₂x − ¹₂ y= −²₃ + b −2 = ²₃ + b b = −2²₃ prosta [AK] y = −²₃ − 2²₃ 0 = − ²₃x − 2²₃ x= − 4 i tak analogicznie zrobiłem dla drugiego punktu

Guma polimer naturalny modyfik: Te pierwsze równanie to układ równań tam coś źle mi się zapisało. −2 = − 1a +b 4 = 3a + b

sushi_ gg6397228: a o Pitagorasie słyszałeś?

Guma polimer naturalny modyfik: Słyszałem i to nie raz, ale jak go tu zastosować?

sushi_ gg6397228: przeciez podali ze trojkat ma byc prostokatny, wiec liczymy długości boków; na potrzeby zadania A= (x;0) |KA|=... |KL|=... |LA|=... i dostaniemy rownanie kwadratowe

Guma polimer naturalny modyfik: AL² = KL² + KA² AL² = ( X_b − X_a )² + ( X_b − X_a )² Skąd wiadomo, które to jest X_b a X_a

Guma polimer naturalny modyfik: AL² = ( X_b − X_a )² + ( Y_b − Y_a )²

sushi_ gg6397228: (5−2)² czy to jest to samo co (2−5)²

sushi_ gg6397228: poza tym w zadaniu podali trójkat KAL− prostokatny, więc kąt prosty jest w wierzchołku o literce ....

Guma polimer naturalny modyfik: Jak mam K = (−1, −2) i L = (3, 4) i A = ( x, 0) to skąd mam wiedzieć co jest X a Y?

sushi_ gg6397228: niech W= (x,y)−−> teraz widac, co to x a co to y

Guma polimer naturalny modyfik: Nie

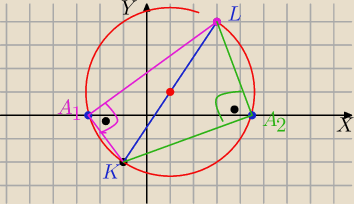
Mila: K = (−1, −2) i L = (3, 4). KL − średnica okręgu

	−1+3		−2+4
S=(		,		)=(1,1)
	2		2

|KL|=√(3+1)²+(4+2)²=√4²+6²=√16+36=√52=2√13 R=√13 A=(x,0) (x−1)²+(y−1)²=(√13)² Punkt przecięcia okręgu z osią OX: (x−1)²+(0−1)²=13 x²−2x+1+1−13=0 x²−2x−11=0 x=1−2√3 lub x=1+2√3 Kąt A₁− kąt prosty jako wpisany w okrąg , oparty na średnicy Kąt A₂− kąt prosty jako wpisany w okrąg , oparty na średnicy A₁=(1−2√3 ,0), A₂=1+2√3

Mila: Powinno być: A₂=(1+2√3,0)

Guma polimer naturalny modyfik: Super naprawdę ci bardzo dziękuję Mila. Teraz już kapuję.

Basia: albo powalczyć z wektorami; będzie o wiele szybciej rysunek taki jak u Mili K = (−1, −20) i L = (3, 4). A(a,0) KA^→ = [a+1; 20] LA^→ = [ a−3; −4] KA^→◯LA^→ = 0 (a+1)(a−3) + 20*(−4) = 0 a² − 3a +a −3 − 80 = 0 a² − 2a − 83 = 0 Δ = 4 + 4*83 = 4(1+83) = 4*84 = 4*4*21 √Δ = 4√21

	2−4√21
a1 =		= 1−2√21
	2

a₂ = 1+2√21 A(1−2√21;0) lub A(1+2√21; 0) ale wynik się nie zgadza; a nie zgadza się bo Mila wzięła K(−1;−2) a ja widzę K(−1;−20) więc jak ma być ?

Mila:

Janek191: Lub forum/210910