geometria
zadanie: Niech Kn oraz Dn beda odpowiednio długosciami najkrótszej i
najdłuzszej przekatnej n−kata foremnego o boku 1. Czy iloraz Dn/Kn
jest liczba całkowita, jezeli
a) n=8 ;
b) n=12 ;
c) n=5 ?
jakies podpowiedzi?
12 wrz 20:23
Mila:
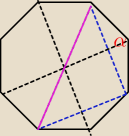
Rysunek i analiza.
α=?
12 wrz 21:03
12 wrz 21:34
12 wrz 21:39
Mila:
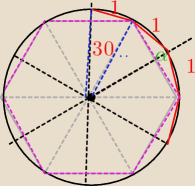
Dwunastokąt foremny.
α=?
Wszystko łatwo policzysz.
12 wrz 21:50
zadanie: α=1080o
x=√2+√2
12 wrz 21:53
zadanie: jutro dokoncze
dziekuje
12 wrz 21:54
Mila:
Pisz , do którego wielokąta są obliczenia.

12 wrz 22:23
zadanie: najpierw pieciokat
tutaj wszystkie przekatne sa tej samej dlugosci wiec iloraz 2 przekatnych jest rowny 1 ∊C
13 wrz 09:25
zadanie: osmiokat foremny
niech K
n=x, D
n=y
α=135
o (wtedy zle policzylem (21:53) bo to byla suma wszystkich katow wewnetrznych)
z tw. cosinusow:
x=
√2+√2
y=
√4+2√2
13 wrz 09:32
zadanie: dwunastokat foremny
α=150
o
z tw. cosinusow:
x=
√2+√3
y=2x=2
√2+√3
13 wrz 09:34
zadanie: mam nadzieje, ze dobrze
13 wrz 09:35
Mila:
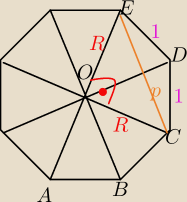
1) Pięciokąt foremny− dobrze.
2) Ośmiokąt foremny − dobry rysunek jest potrzebny i analiza. ( na liczenie zawsze jest czas)
3)d=2R − najdłuższa przekątna jest równa 2 promieniom (R) okręgu opisanego na tym ośmiokącie.
4) p=R
√2 − najkrótsza przekątna ośmiokąta foremnego jest przeciwprostokątną w równoramiennym
Δ prostokątnym o przyprostokątnych równych R.
W takim razie :
(obliczenia długości przekątnych masz dobrze)
13 wrz 18:46
Mila:
Dwunastokąt foremny.
1) rysunek, analiza i odpowiedź bez obliczeń− czekam.
Obliczenia masz dobrze.
13 wrz 18:55
Mila:
I jeszcze jedno, oblicz długość przekątnej pięciokąta foremnego o boku długości a, bez
trygonometrii.
13 wrz 18:57
zadanie: kat wewnetrzny pieciokata foremnego wynosi 1080 wiec trudno obliczyc cos tego kata wiec z
trygonometria byloby trudniej
13 wrz 19:09
zadanie: sprobuje pomyslec
13 wrz 19:10
zadanie: a odnosnie dwunastokata foremnego to mam narysowac rysunek i go omowic?
13 wrz 19:11
Mila:
1) Jeśli chodzi o dwunastokąt, to masz "widzieć" , dlaczego proszę o odpowiedź bez obliczeń.
2) Pięciokąt. Dobry rysunek, opisać kąty, skorzystać np. z tw. o dwusiecznej kąta 720,
otrzymasz złotą proporcję.
13 wrz 19:20
zadanie: z rysunku 21:50 widac, ze najkrotsza przekatna to bok trojkata rownobocznego (bo dwunastokat
foremny sklada sie z szesciokata foremnego, ktory jest zbudowany z 6 trojkatow rownobocznych)
oraz rowniez mozna zauwazyc, ze najdluzsza przekatna to jeden bok trojkata rownobocznego z
jedej strony i jeden bok trojkata z drugiej strony czyli 2 razy ten sam bok.
13 wrz 19:22
Mila:
Dobrze. Komentarz w nawiasie nie podoba mi się, ale wiem, co chciałeś powiedzieć.
1) najdłuższa przekątna: d=2R,
R− promień okręgu opisanego na dwunastokącie foremnym.
2) najkrótsza p=R, jako bok Δ równobocznego.
13 wrz 19:35
zadanie:
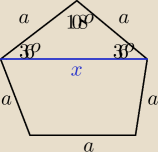
x−przekatna pieciokata
13 wrz 20:03
zadanie: chyba jutro pomysle
13 wrz 20:16
Mila:

13 wrz 21:09
zadanie: juz zrobilem napisze za jakis czas
14 wrz 10:52
zadanie: niech:
p− przekatna pieciokata
FB=x=FC
AF=p−x=DF
AF−dwusieczna kata 72
o
z tw. o dwusiecznej:
trojkaty ABC i BCF sa podobne ze wzgledu na katy
po przyrownaniu obu x:
ap
2−a
2p−a
3=0 ; a>0
Δ=5a
4;
√Δ=a
2√5
dobrze?
14 wrz 11:54
zadanie: ?
14 wrz 21:50
Mila:
Dobrze.
Uwagi:
1) Można :
ap
2−a
2p−a
3=0 ; a>0 /:a
p
2−ap−a
2=0
i wyjdzie to samo.
2) mogłeś zauważyć, że DF=DC=a
wtedy:
z tw. o dwusiecznej:
p*(p−a)=a
2
p
2−ap−a
2=0
Zadanie 2.
Teraz oblicz wartości:
cos36
0
cos72
0
sin18
0
14 wrz 22:25
zadanie: no wlasnie bo znajac te wartosci mozna by to obliczyc szybciej z twierdzenia cosinusow
ale juz jutro to sprobuje obliczyc
14 wrz 22:38
Mila:
Zobacz zadania 'Diamentowy indeks" AGH− 2013/2014rok.
14 wrz 23:06
zadanie: spobuje zrobic to zadanie ale najpierw mam jeszcze 4 albo 5 zadan, ktore tez chce zrozumiec
napisze je w innym poscie
na poczatku da sie zauwazyc, ze cos36o=sin54o oraz cos72o=sin18o
zadanie zeby obliczyc sin18o jest nawet na tej stronie patrzylem troche na to i na pierwszy
rzut oka troche inne niz dotychczas pozniej sprobuje to poobliczac
zadania z tej olimpiady sa bardzo ciekawe i takich nie robilo sie w szkole ale na wziecie
udzialu w takiej olimpiadzie jest troche za pozno bo juz jestem po maturze
15 wrz 12:04
zadanie: w tym rozwiazaniu zostalo obliczone wyrazenie cos36osin18o ja bym nie wiedzial, ze trzeba to
obliczyc
zobaczylem w internecie i tam jest to prosciej zrobione za pomoca wzorow trygonometrycznych
jutro to jeszcze przeanalizuje i napisze
16 wrz 00:08
zadanie: za pomoca internetu obliczylem sin18 oraz cos36 i cos18
wykorzystalem wzory:
sin2α=2sinαcosα
cos2α=1−2sin
2α
cos(α+β)=cosαcosβ−sinαsinβ
cosα=sin(90−α)
sin36=cos54=cos36+18
sin36=cos36+18
2sin18cos18=cos36cos18−cos36sin18
2sin18cos18=cos18*(1−2sin
218)−2sin18cos18sin18/cos18
4sin
218+2sin18−1=0
t=sin18; t∊(0,1)
4t
2+2−1=0
Δ=20;
√Δ=2
√5
16 wrz 18:45
Mila:
Masz tam błędne zapisy.
Nie o to mi chodziło.
Masz w pięciokącie foremnym odpowiednie trójkąty, stamtąd oblicz wartości cosinusa. Masz
obliczoną przekątną.
Rysunek 21:09.
16 wrz 19:09
zadanie: Z tw. cosinusow
| | p2−2a2 | | a(√5+1 | |
cos108o= |
| , gdzie p= |
| |
| | −2a2 | | 2 | |
| | −a2+a2√5 | | 1 | | −a2+a2√5 | | −√5+1 | |
cos108o= |
| * |
| = |
| = |
| |
| | 2 | | −2a2 | | −4a2 | | 4 | |
cos108
o=cos(90
o+18
o)=−sin18
o
a co wtedy bylo zle zapisane?
16 wrz 22:01
Mila: Zamiast : sin36=cos54=cos36+18 ma być sin36=cos54=cos(36+18 )
Zamiast: sin36=cos36+18 ma być:sin36=cos(36+18 )
WΔ DBC:
p
2=a
2+a
2−2a
2cos108⇔p
2=2a
2−2a
2cos108
p
2=2a
2(1−cos108)
| a2*(1+√5)2 | |
| =2a2*(1−cos108) /:a2 |
| 4 | |
| 6+2√5 | |
| =2(1−cos(108)) /:2 |
| 4 | |
| √5−1 | |
| =−cos(1080)=sin(180) |
| 4 | |
cos(108)=cos(180−72)=−cos(720)
W ΔABD:
a
2=p
2+p
2−2p
2*cos 36
0
Dokończ i zapisz wszystkie obliczenia.
16 wrz 22:29
zadanie: | | a2(1+√5)2 | | 5a2+2a2√5+a2 | | 6a2+2a2√5 | |
p2= |
| = |
| = |
| = |
| | 4 | | 4 | | 4 | |
| 2(3a2+a2√5) | | 3a2+a2√5 | |
| = |
| |
| 4 | | 2 | |
W ΔABD:
a
2=p
2+p
2−2p
2*cos36
o
2p
2−2p
2cos36
o=a
2
−2p
2cos36
o=a
2−2p
2
| | a2−3a2−a2√5 | | −2a2−a2√5 | |
= |
| = |
| = |
| | −3a2−a2√5 | | −3a2−a2√5 | |
| | 2+√5 | | 3−√5 | | 6−2√5+3√5−5 | | 1+√5 | |
= |
| * |
| = |
| = |
| =sin54o |
| | 3+√5 | | 3−√5 | | 9−5 | | 4 | |
17 wrz 09:16
 Rysunek i analiza.
α=?
Rysunek i analiza.
α=?
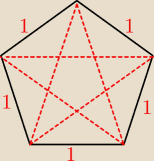 Ciekawy pięciokąt foremny.
http://pl.wikipedia.org/wiki/Pi%C4%99ciok%C4%85t
Ciekawy pięciokąt foremny.
http://pl.wikipedia.org/wiki/Pi%C4%99ciok%C4%85t
 Dwunastokąt foremny.
α=?
Wszystko łatwo policzysz.
Dwunastokąt foremny.
α=?
Wszystko łatwo policzysz.

 1) Pięciokąt foremny− dobrze.
2) Ośmiokąt foremny − dobry rysunek jest potrzebny i analiza. ( na liczenie zawsze jest czas)
3)d=2R − najdłuższa przekątna jest równa 2 promieniom (R) okręgu opisanego na tym ośmiokącie.
4) p=R√2 − najkrótsza przekątna ośmiokąta foremnego jest przeciwprostokątną w równoramiennym
Δ prostokątnym o przyprostokątnych równych R.
W takim razie :
1) Pięciokąt foremny− dobrze.
2) Ośmiokąt foremny − dobry rysunek jest potrzebny i analiza. ( na liczenie zawsze jest czas)
3)d=2R − najdłuższa przekątna jest równa 2 promieniom (R) okręgu opisanego na tym ośmiokącie.
4) p=R√2 − najkrótsza przekątna ośmiokąta foremnego jest przeciwprostokątną w równoramiennym
Δ prostokątnym o przyprostokątnych równych R.
W takim razie :
 x−przekatna pieciokata
x−przekatna pieciokata
