Geometria analityczna Prosta m tworzy z osią x kąt o mierze... Koral: Prosta m tworzy z osią x kąt o mierze 30^o i przechodzi przez punkt P=(3, −1). Prosta k jest prostopadła do prostej m i przecina oś x w tym samym punkcie co prosta m. a) wyznacz równanie prostej m i k b) oblicz pole trójkąta ograniczonego prostymi m, k i osią y. Zawsze tylko pierwsza liczba jest pod kreską ułamkową. Ja obliczyłem:

	√3
a=tg30=
	3

	√3x
−1=
	3

	√3
Prosta m y=		−1−√3
	3

i dalej liczyłem dla pr. k

	−3x
y=		+b
	√3

	−3*3
−1=		+b
	√3

b=−1−3√3 Prosta k y=−√3x−1−3√3 a powinno wyjść y=−√3x+3+3√3 Następnie nie mam zielonego pojęcia jak obliczyć pole.

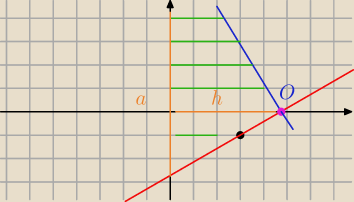
Aga1.: Prosta k nie przechodzi przez punkt P, tylko przez O

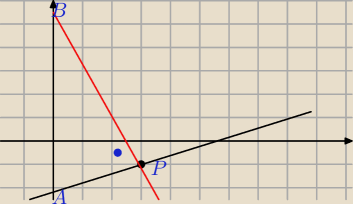
Basia: wyniki masz prawie dobre, ale nie do końca więc jeszcze raz

	√3
a = tg30 =		to jest dobrze
	3

ale dalej już nie

	√3
y =		x + b
	3

	√3
−1 =		*3 + b
	3

b = −1−√3

	√3
m: y =		x −1 − √3
	3

k⊥m k: y = −√3x + b −1 = −3√3 + b b = −1+3√3 k: √3x − 1 + 3√3 A(0; −1−√3) B(0, −1+3√3) tr.APB jest prostokątny

	|AP|*|BP|
P =
	2

Basia: aj faktycznie oś przecina w tym samym punkcie trzeba to jeszcze raz policzyć

Koral: Super proste już obliczyłem wielkie dzięki za pomoc. Teraz tylko nie wiem jak obliczyć to pole jest na to jakiś wzór bo u mnie w książce nic nie znalazłem ani tutaj na tej stronie.

Koral: Wynik pola 8√3 + 12

Koral: Już wiem jak pole obliczyć korzystając z osi, ale gdyby nie było osi jest na to jakiś inny sposób? wzór?