Pochodna. Styczna - znaleźć wzór... I_love_PI: Cześć! Proszę o pomoc Dwie proste styczne do wykresu funkcji f(x)=x² przecinają się pod kątem prostym w punkcie na osi OY. Znajdź równania tych prostych. wiem, że a * a₁=(−1), gdzie f^'(x)=2x równania stycznych: y= ax+b y₁=a₁x+b, obie styczne muszą, wg mnie mieć to samo przecięcie na OY, czyli to samo b tylko co dalej... pomożecie?

I_love_PI: proszę niech ktoś tu looknie

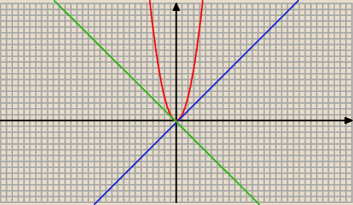Janek191: f(x) = x² Te proste mają równania: y = x + b i y = − x + b Mają być styczne do wykresu funkcji f(x) = x² więc muszą mieć jeden punkt wspólny x + b = x² x² − x − b = 0

	1
Δ = ( −1)2 − 4*1*( −b) = 1 + 4b = 0 ⇒ b = −
	4

czyli

	1
y = x −
	4

oraz

	1
y = − x −
	4

I_love_PI: Janek191 − dzięki za pokazanie co i jak, ale jednak mam pewną wątpliwość − dlaczego od razu zakładasz, że te styczne mają współczynniki kierunkowe 1 i −1? Skąd wiesz, że właśnie takie wartości?

Janek191: tg 45^o = 1 = a₁ tg ( − 45⁰ ) = tg ( 135^o) = − 1 = a₂ 1*(−1) = − 1 lub 135^o − 45^o = 90^o Proste o tych współczynnikach są prostopadłe i symetryczne względem osi OY. Aby były styczne do paraboli o równaniu y = x² muszą mieć jeden punkt wspólny z tą parabolą, czyli x + b = x² ⋀ − x + b = x² np. − x + b = x² x² + x − b = 0

	1
Δ = 12 − 4*1*(−b) = 1 + 4b = 0 ⇒ b = −
	4

	1
czyli y = − x −
	4

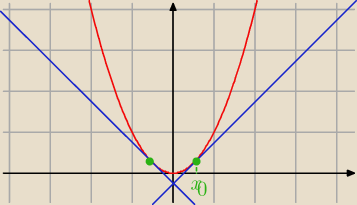Aga1.: a=f^'(x₀)=2x₀ a₁=f^'(−x₀)=−2x₀ 2x₀*(−2x₀)=−1 −4x₀²=−1

	1		−1
xo=		lub x0=		,
	2		2

więc

	1
a=2*		=1
	2

lub a=−1

I_love_PI: dzięki, no właśnie ! już wiem, dzięki wielkie dla wszystkich