Udowadnianie THIRTEEN_13: Jak udowodnić że :

	π		2π		1
a) cos		* cos		=
	5		5		4

	π		3π		1
b) cos		* cos		= −
	5		5		4

THIRTEEN_13:

PW:

	π		√5+1
cos		=cos36°=
	5		4

	2π		√5−1
cos		=cos72°=
	5		4

Wartości te są znane, można je znaleźć w tablicach. Jak je obliczyć, to już inne zadanie.

THIRTEEN_13: No właśnie ja bym chciał wiedzieć jak te wartości można obliczyć

PW: Pokombinuj, np. pożyteczne może być spostrzeżenie, że 72+18=90 i 72=4•18.

Bogdan: Proponuję tak:

	π		2π		π   2*2sin   5
cos		cos		*		=
	5		5		π   2*2sin   5

	2π   2π   2sin cos   5   5		4π   sin   5
=		=		=
	π   4sin   5		π   4sin   5

	π   sin(π − )   4		π   sin   4		1
=		=		=
	π   4sin   5		π   4sin   5		4

Bogdan: drugi przykład analogicznie

PW: Bogdan − a tak się dobrze zaczynaliśmy bawić − THIRTEEN₋13 chciał właśnie obliczyć cos36° i twierdził, że jest mu to potrzebne. Niechby wyliczył, zachęcam − to pożyteczne ćwiczenie. Swoją drogą świetny pomysł (z gatunku tych, co to uczniowie mówią "a skąd ja niby miałbym być taki mądry?").

Bogdan:

THIRTEEN_13: Mógłbyś podsunąć pomysł

Piotr 10: Bogdan lub PW możecie tutaj zajrzeć https://matematykaszkolna.pl/forum/210862.html ?

PW: ’Pomysł na policzenie sin72° = cos18° sin4α=2sin2αcos2α=4sinαcosα(1−2sin²α) cos18°=4sin18°cos18°(1−2sin²18°) 1=4sin18°(1−2sin²18°) 1=4x(1−2x²) 8x³−4x+1=0 Tu słaby punkt tego pomysłu, bo nie umiem pokazać jak dojść do rozwiazania tego równania. matematycy w takiej sytuacji mowią:

	√5−1
Jak łatwo sprawdzić rozwiązaniem jest x=		.
	4

Może ktoś podsunie zgrabniejszy pomysł, ale na tego typu równaniach polega policzenie funkcji trygonometrycznych kątów 72°, 36°,22,5°, 54°

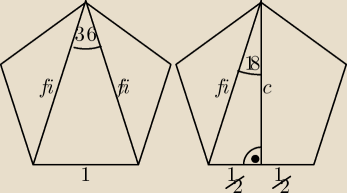
Bogdan: Pięciokąt foremny.

	1 + √5
fi = φ =		to złota liczba
	2

	2φ2 − 1
Z tw. cosinusów: 1 = 2φ2 − 2φ2cos36o ⇒ cos36o =
	2φ2

	√φ2 − 0,52
c = √φ2 − 0,52 , cos18o =
	φ

Janek191: @ Bogdan Tam w licznika ( ostatni wiersz ) powinno być

	π		π
sin( π −		) i sin
	5		5

PW: Bogdan wiedziałem, że jest czysto geometryczny sposób, ale nie przypomniałem go sobie. Teraz każdy widzi (ja stary sklerotyk też). 3•180°=540°

	540°
		=108°
	5

(to napisałem dla siebie, żeby sobie utrwalić, reszta już jasna)

Bogdan: Dziękuję Janek191 za poprawienie chochlika To jest nas PW − starych sklerotyków więcej

Antek: No tak . Ledwo przekroczyli trzydziestke i juz starzy . Bez obrazy . Stare ale chyba osly

PW: Antek, niedługo Twoja wnuczka i mój wnuk spotkają się na studiach. Ja tutaj się udzielam tylko dlatego, że stwierdziłem zaniki pamięci (wedle dziadzi Darwina narządy nieużywane zanikają).

Mila: Do Trzynastego. 1) Oblicz długość przekątnej pięciokąta foremnego, bez trygonometrii. 2) Dobry rysunek, opisać kąty, skorzystać np. z tw. o dwusiecznej kąta 72⁰, otrzymasz złotą proporcję. Proszę szanownych kolegów , aby nie rozwiązywali, jest piątek , jest czas, młody kolega popróbuje swoich sił. Będziemy podpowiadać.