geometria zadanie: Czy istnieje czworokat wypukły o bokach podanej długosci (z zachowaniem kolejnosci), którego przekatne sa prostopadłe a) 6, 5, 2, 4 ? jaki warunek musi byc spelniony? nie bedzie to kwadrat ani romb przekatne sa prostopadle w deltoidzie

Bogdan: Istnieją także trapezy posiadające prostopadłe do siebie przekątne.

zadanie: no dobrze ale jaki warunek musza spelnic te dlugosci bokow?

zadanie: ?

Bogdan: a jakie są Twoje przemyślenia w tej sprawie, bo widzę, że oczekujesz gotowej recepty

zadanie: ja myslalem o deltoidzie bo tam przekatne sa prostopadle i w kazdy deltoid mozna wpisac okrag ale przeciez nie tylko w deltoidzie przekatne sa prostopadle wiec to raczej nie moze byc tak

Bogdan: Narysuj dowolny czworokąt wypukły i jego przekątne, przekątne są prostopadłe. Wprowadź oznaczenia literowe na długości boków i przekątnych, oznacz kąty proste i zagoń do roboty Pitagorasa dla powstałych w czworokącie trójkątów prostokątnych.

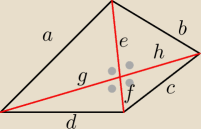
zadanie: a²=e²+g² b²=e²+h² c²=f²+h² d²=g²+f² ale za duzo tych niewiadomych

zadanie: jakas podpowiedz co dalej ?

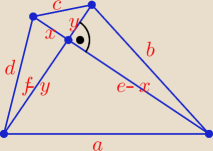
Bogdan: Tu nie ma niewiadomych, są tylko oznaczenia. Spróbuj tak oznaczyć: a, b, c, d − długości boków czworokąta wypukłego (jak na rysunku), e, f − długości przekątnych tego czworokąta, przekątne są do siebie prostopadłe.

Bogdan: Korzystając z twierdzenia Pitagorasa: x² + y² = c² x² + (f − y)² = d² ⇒ x² + f² − 2fy + y² = d² ⇒ f² − 2fy = d² − c² y² + (e − x)² = b² ⇒ y² + e² − 2ex + x² = b² ⇒ e² − 2ex = b² − c² + −−−−−−−−−−−−−−−− (*) e²−2ex+f²−2fy=b²+d²−2c² (e−x)² + (f−y)² = a² ⇒ e²−2ex+x²+f²−2fy+y² = a² ⇒ e²−2ex+f²−2fy=a²−c² (**) Porównując prawe strony równości (*) i (**) otrzymujemy: b²+d²−2c² = a²−c² ⇒ a² + c² = b² + d² Sformułuj wniosek

zadanie: aby przekatne czworokata wypuklego byly prostopadle musi zachodzic rownosc a²+c²=b²+d²

Bogdan: Sformułuj wniosek pełnymi słowami, bez tekstu a² + c² = b² + d² (można przecież użyć innych literek do zapisu tej równości).

zadanie: aby przekatne czworokata wypuklego byly prostopadle to sumy kwadratow przeciwleglych bokow musza byc rowne o to chodzilo?

zadanie: ?

Bogdan: nie sumy kwadratów przeciwległych boków, a sumy kwadratów długości przeciwległych boków ...

zadanie: dziekuje