 Ta całka to całka krzywoliniowa skierowana. Zakładamy dodatnią orientację krzywej (skierowanie
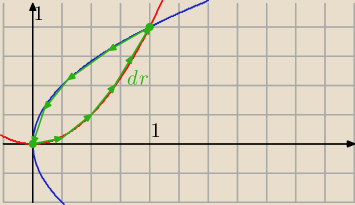
wektora dr przeciwnie do ruchu wskazówek zegara). Całkę policzymy wprowadzając
parametryzację. Na odcinku czerwonym obowiązuje parametryzacja y = x2. Z kolei na odcinku
niebieskim mamy y = √x. Granice można łatwo odczytać z rysunku. Zatem:
Ta całka to całka krzywoliniowa skierowana. Zakładamy dodatnią orientację krzywej (skierowanie
wektora dr przeciwnie do ruchu wskazówek zegara). Całkę policzymy wprowadzając
parametryzację. Na odcinku czerwonym obowiązuje parametryzacja y = x2. Z kolei na odcinku
niebieskim mamy y = √x. Granice można łatwo odczytać z rysunku. Zatem:
| 1 | 2 | 1 | ||||
∫K ydx = ∫01 x2dx + ∫10 √xdx = | − | = − | . | |||
| 3 | 3 | 3 |