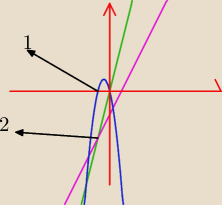
czx marcin: Witam mam do obliczenia pole oszaru z trzech funkcji zielona y=2x rozowa y=x−2 niebieska y=1−(x+1)² punkt 1 (−2;0) punkt 2 (−2,−4) Mam problem z wyznaczeniem ganic calkowania bo zapomnialem jak to sie robi... Pamietam tylko ze bylo cos ze funkcja ograniczajaca z dolu i z gory ale co do czego to nie pamietam, Jakby ktos mogl mi pomoc na podstawie tego rysunku to byłbym wdzieczny pozdrawiam

wredulus_pospolitus: krok 1: zaznacz sobie na kartce obszar którego pole chcesz policzyć krok 2: wyznacz 'x' które są w punkcie 'najbardziej na lewo i prawo' tego obszaru (granice całkowania) krok 3: napisz całkę ... w całce zrób różnicę: funkcja której wykres jest "wyżej" − funkcja która jest "niżej"

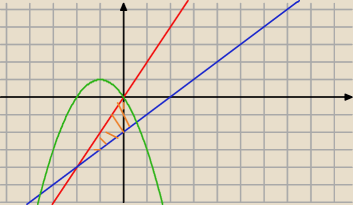
fx: Granice całkowania to rozpiętość obszaru na osi OX. Obszar ograniczony przez te krzywe zaznaczyłem na pomarańczowo. Widać od razu, że należy rozwiązać w celu wyznaczenia granic dwa równania: 2x = x−2 oraz 1−(x+1)² = x−2 Całkujesz w granicach (a;b) różnicę funkcji graniczącej obszar z góry i funkcji ograniczającej z dołu.

wredulus_pospolitus: fx ... jesteś pewien że o ten obszar chodzi bo opis (współrzędne punktów) który podał autor sugeruje jednak na obszar po lewej

fx: U, rutyna... Nie zwróciłem uwagi na te punkty.

marcin: czyli Panowie jak w końcu to ma być ktory obszar mam policzyc Dolna granica bedzie −2 a gorna 0

marcin: punkt w ktorym przecina sie funkcja niebieska z zielona ponizej osi x to (−4,−8)

marcin: pomocy...

Basia: no przecież wredulus Ci to narysował 1−(x+1)² = 1 − x² − 2x − 1 = −x²−2x −x²−2x = x−2 −x² − 3x + 2 = 0 x² + 3x − 2 = 0 Δ=9+8 = 17

	−3−√17
x1 =
	2

	−3+√17
x2 =
	2

P = ₂∫⁰(2x−(x−2))dx + ₀∫^x₂ [−x²−2x − (x−2)] dx dość paskudne, ale da się policzyć na pewno dobrze przepisałeś wzory funkcji ?

wredulus_pospolitus: marcin ... a skąd mamy wiedziec KTÓRY obszar masz obliczyć ... są tutaj dwie 'opcje' i Ty powinieneś wiedzieć który obszar to jest a nie my

Basia: witaj wredulus ten drugi będzie miał tak samo paskudną dolną granicę całkowania; to będzie x₁

marcin: Wzory funkcji są na pewno dobrze napisane. Czyli jak jest taki przypadek to trzeba liczyć obydwa obszary tak

Basia: sądzę, że tak