bryła karmelka: trapez równoramienny o podstawach a i 2a i kącie ostrym α obraca się wokół ramienia. I mam obliczyć objętość i pole całkowite powstałej bryły. myślę że dam radę to zrobić ale nie umiem sobie wyobrazić jak ta bryła będzie wyglądać pomóżcie, wytłumaczcie lub narysujcie jak to będzie wyglądać proszę

dero2005:

karmelka: ojoj. . . no dobra, ale już wiem jak to wygląda xD dziękuję

karmelka: no dobra jednak potrzebuję pomocy... może ktoś mi rozpisać to zadanie?

dero2005:

	2a−a		a
x =		=
	2		2

x
	= cosα
c

	x		a
c =		=
	cosα		2cosα

R
	= sinα
2a

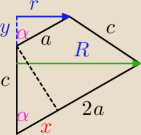R = 2asinα

r
	= sinα
a

r = asinα

y
	= {cosα}
a

y = acosα

karmelka: ok, ale z tych danych nadal nie policzę objętości i pola całkowitego. Da się policzyć objętość stożka tego dużego ( z trójkąta R, 2a, c) i i tego wyciętego mniejszego stożka ( y, r, a) A co z tym fragmentem który nie jest ani tym dużym ani tym mniejszym stożkiem

karmelka: poza tym trapez może byćteż tak ułożony (że dłuższ podstawa będzie wychodziła ponad krawędzie boczne i krótszą podstawę). Co w takim wypadku

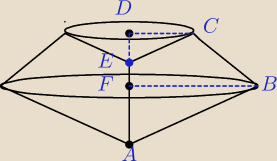
dero2005: AB = 2a

	a
BC =
	2cosα

CD = asinα FB = 2asinα CE = a FA = 2acosα DE = acosα FE = CB−FA FD = FE+DE Policz objętość stożka ściętego BCDF o promieniu R=FB i r = DC i wysokości FD do tego dodaj objętość stożka ABF o promieniu R = BF i wysokości AF i odejmij objętość stożka CDE o promieniu podstawy r = CD i wysokości ED Przy polu powierzchni oblicz pole boczne stożka ściętego BCDF, dodaj pole boczne stożka ABF i dodaj pole boczne stożka CDE