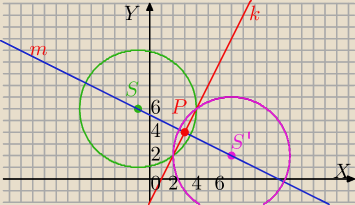
 x2 +2x+y2−12y+12=0 względem prostej y=2x−2
Przedstawiamy równanie okręgu w postaci kanonicznej
(x+1)2−1+(y−6)2−36+12=0⇔
(x+1)2+(y−6)2=25⇔(x+1)2+(y−6)2=52⇔
S=(−1,6) i r=5
Obrazem okręgu w symetrii względem prostej
k: y=2x−2 będzie okrąg o promieniu r'=5, środek S' należy wyznaczyć
Środek leży na prostej prostopadłej do k i przechodzącej przez punkt S
m⊥k
x2 +2x+y2−12y+12=0 względem prostej y=2x−2
Przedstawiamy równanie okręgu w postaci kanonicznej
(x+1)2−1+(y−6)2−36+12=0⇔
(x+1)2+(y−6)2=25⇔(x+1)2+(y−6)2=52⇔
S=(−1,6) i r=5
Obrazem okręgu w symetrii względem prostej
k: y=2x−2 będzie okrąg o promieniu r'=5, środek S' należy wyznaczyć
Środek leży na prostej prostopadłej do k i przechodzącej przez punkt S
m⊥k
| −1 | 1 | 1 | ||||
m: y= | x+b i 6= | +b, b=5 | ||||
| 2 | 2 | 2 |
| −1 | 1 | |||
m:y= | x+5 | |||
| 2 | 2 |
| −1 | 1 | ||
x+5 | =2x−2⇔x=3 i y=4⇔P=(3,4) środek SS'. S'=(xs,ys)⇔ | ||
| 2 | 2 |
| xs+(−1) | ys+6 | |||
3= | i 4= | stąd | ||
| 2 | 2 |
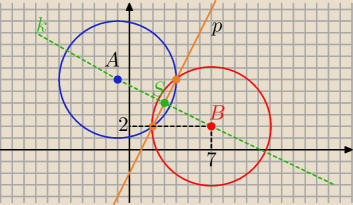 o: (x−7)2+(y−2)2=25
o: (x−7)2+(y−2)2=25