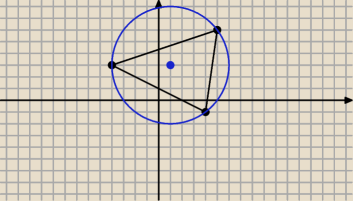
geometria karolina: Znajdź równanie okręgu opisanego o wierzchołkach A(−4,3) B(4,−1) C(5,6) proszę o pomoc bo mi nie wychodzi

dero2005: (−4−a)² + (3−b)² = r² 1 (4−a)² + (3−b)² = r² 2 (5−a)² + (6−b)² = r² 3 od 1 odjąć 2, od 2 odjąć 3 2a − b = −1 a+7b = 22 a = 1 b = 3 r² = 25 (x−1)² + (y−3)² = 25

kajka: DZIEKUJE

Antek: Lub mozna tez zrobic tak 1. Napisac rownanie symetralnej AB 2. Napisac rownanie symetralnej Ac 3. Wyznaczyc punkt przeciecia sie obu symetralnych (bedzie to srodek okregu opisanego na trojkacie ) i oznaczyc go przez O 4. Policzyc dlugosc odcinka AO − bedzie to promien tego okregu 5.Mamy juz wszystko zeby napisac to rownanie. MOj sposob jest dluzszy ale mozna sobie pocwiczyc rozne wzory i np pocwiczyc wektory . rownanie prostych w postaci ogolnej a nie tylko kierunkowej ,zauwazyc z edlugosc odcika to dlugosc wektora