FUNKCJA ODWROTNA lokinek: Czy funkcja odwrotna do f: y=√x − 2 − 2 w przedziale <2,+n) to f⁻¹: y=x² + 2x + 3

sushi_ gg6397228: aby sprawdzic zrób złożenia f o f⁻¹= x

asdf: y = √x−2 − 2 y + 2 = √x−2 y² + 4y + 4 = x − 2 y² + 4y + 6 = x ⇒ f⁻¹: y = x² + 4y + 6 chyba coś takiego

lokinek: przepraszam jest błąd. Pierwotna funkcja wygląda tak: y=√x−2 − 1 osią symetrii ma być prosta y=x i to jakoś mi nie wychodzi na wykresie

PW: No tak, mówiąc "po chamsku" trzeba wyliczyć iksa za pomocą igreka, a potem mechanicznie zamienić x na y i y na x, bo jesteśmy przyzwyczajenie do tego, że argument nazywa się x, a wartość funkcji to y.

lokinek: chyba jest dobrze, tylko że jest to funkcja w przedziale i te wykresy nie koniecznie wyglądają na symetryczne. są też dość duże liczby więc ciężko to w zeszycie narysować

PW: A jakie było polecenie: "wyznacz wzór i narysuj wykres funkcji odwrotnej", czy tylko "narysuj wykres funkcji odwrotnej"?

lokinek: wyznacz wzór i narysuj wykres podana funkcja: y=√x−2 −1

PW: Tak jak asdf to zrobił, wynik masz dobry: y=x²+2x+3

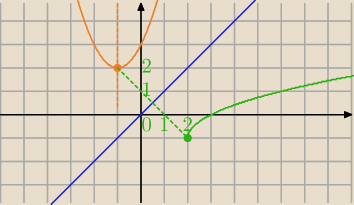
Mila: f(x)=√x−2−1 y=x²+2x+3

	−2
xw=		=−1
	2

Interesuje Cię tylko ta część paraboli dla x≥−1

PW: Mila, teraz dopiero zrozumiałem, dlaczego lokinek pisala "te wykresy nie koniecznie wyglądają na symetryczne". Zapomniała o dziedzinie?