Równanie kwadratowe z parametrem.
Wika: 1.Dla jakich wartości parametru m równanie ma dwa różne pierwiastki?
x2+(2m+1)x+5=0
2.Określ liczbę pierwiastków równania w zależności od parametru m.
x2+(m−1)x+2m−5=0
10 wrz 20:22
Wika: Proszę o pomoc..

10 wrz 20:30
Lorak: problem z obliczeniami czy w ogóle nie wiesz jak się zabrać za to ?
10 wrz 20:37
ICSP: a od czego zależy ilość pierwiastków w równaniu kwadratowym ?
10 wrz 20:37
Mila:
1) warunek:
Δ>0
2)
Δ=0 jeden pierwiastek podwójny
Δ>0 dwa różne pierwiastki
Δ<0 brak pierwiastków rzeczywistych.
10 wrz 20:39
Wika: No to w pierwszym mi wyszło
Δ=b2−4ac
Δ=(2m+1)2−4*1*5
Δ=4m2+4m−19
Δ>0
4m2+4m−19
a=4 b=4 c= −19
Δ=16−4*4*(−19)
Δ=16+304
Δ=320>0
i co dalej, czy coś tu źle zrobiłam
a tego drugie wgl. nie mogę zrobić bo nie ogarniam
10 wrz 20:45
Wika: Może ktoś mi to wytłumaczyć jak mam to wszystko zrobić krok po kroku?
10 wrz 20:56
ICSP: No wiec tak :
f(x) = x2 + (2m+1)x + 5
mamy wyznaczyć dla jakich m to równanie będzie miało dwa różne pierwiastki
równanie kwadratowe ma dwa rożne pierwiastki gdy Δ > 0
zatem :
Δ = (2m+1)2 − 4*1*5 = 4m2 + 4m − 19
Δ> 0 ⇒ 4m2 + 4m − 19 > 0
Czyli całe zadanie sprowadza się do rozwiązania nierówności kwadratowej :
4m2 + 4m − 19 > 0
Potrafisz rozwiązywać nierówności kwadratowe ?
10 wrz 20:59
Wika: do tego momentu też zrobiłam, dalej ni hu hu
10 wrz 21:00
ICSP: ale co później trudnego jest ?
liczysz Δ
m
Liczysz miejsca zerowe jeśli istnieją
Rysujesz parabole i dajesz odp

10 wrz 21:03
dero2005:
4m2+4m−19>0
rozwiąż nierówność
10 wrz 21:05
Mila:
1)
x
2+(2m+1)x+5=0
Δ=(2m+1)
2−4*5=4m
2+4m+1−20=4m
2+4m−19
Równanie ma dwa różne pierwiastki dla
4m
2+4m−19>0
Δ
m=16−4*4*(−19)=16+16*19=320
√320=
√16*20=4
√20=4
√4*5=8
√5
| | −4−8√5 | | −4+8√5 | |
m1= |
| lub m2= |
| ⇔ |
| | 8 | | 8 | |
| | −1−2√5 | | −1+2√5 | |
m1= |
| lub m2= |
| |
| | 2 | | 2 | |
| | −1−2√5 | | −1+2√5 | |
⇔Δ>0 dla m< |
| lub m> |
| |
| | 2 | | 2 | |
10 wrz 21:05
Wika: Δm?
czyli wzór jak na zwykłą Δ?
niestety dziś miałam dopiero 1 lekcję z równań z parametrem
10 wrz 21:09
dero2005:
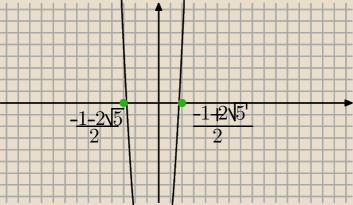
10 wrz 21:14
dero2005:
| | −1−2√5 | | −1+2√5 | |
m∊(−∞, |
| ) U ( |
| , ∞) |
| | 2 | | 2 | |
10 wrz 21:17
Wika: Dziękuje bardzo za to pierwsze.
A teraz będzie ktoś tak wytrwały i pomoże mi przy tym drugim?
10 wrz 21:21
Mila:
2) rozwiązujesz podobnie.
10 wrz 21:26
dero2005:
Δ = (m−1)2 − 4*1*(2m−1)
Δ = m2 − 10m + 21
gdy
m2 − 10m + 21 > 0 dwa pierwiastki różne
gdy
m2 − 10m + 21 = 0 jeden pierwiastek (podwójny)
gdy
m2 − 10m + 21 < 0 brak pierwiastów
liczysz każdy przypadek
10 wrz 21:38
ZKS:
x
2 + (m − 1)x + 2m − 5 = 0
| | (m − 1)2 | | (m − 1)2 | |
x2 + (m − 1)x + |
| − |
| + 2m − 5 = 0 |
| | 4 | | 4 | |
| | m − 1 | | (m − 1)2 − 8m + 20 | |
(x + |
| )2 − |
| = 0 |
| | 2 | | 4 | |
| | m − 1 | | m2 − 2m + 1 − 8m + 20 | |
(x + |
| )2 = |
| |
| | 2 | | 4 | |
| | m − 1 | | m2 − 10m + 21 | |
(x + |
| )2 = |
| |
| | 2 | | 4 | |
| | m − 1 | | √m2 − 10m + 21 | |
x + |
| = ± |
| |
| | 2 | | 2 | |
Pierwiastek parzystego stopnia z liczby ujemnej nie istnieje więc
jeżeli m
2 − 10m + 21 < 0 mamy brak rozwiązań
jeżeli m
2 − 10m + 21 = 0 mamy jeden pierwiastek
jeżeli m
2 − 10m + 21 > 0 mamy dwa pierwiastki.
10 wrz 21:39
Tomek: a jak mam ten każdy przypadek liczyć?
10 wrz 21:54
Wika: o widzę ktoś tu mi się wcina w prace domową

10 wrz 21:55
Mila:
m
2 − 10m + 21 > 0 dwa pierwiastki różne
Δ
m=100−4*21=16
| | 10−4 | | 10+4 | |
m1= |
| =3 lub m= |
| =7 |
| | 2 | | 2 | |
i rozwiązuj nierówność ,
10 wrz 21:59
dero2005:
m
2 − 10m + 21 < 0
Δ = 100 − 84 = 16
√Δ = 4
m∊( 3, 7) dla tych wartości m pierwiastki nie istnieją
itd
10 wrz 21:59



