F. Kwadratowa Piotr 10: Dla jakich wartości parametru m nierówność (x−3m)(x−m−3) < 0 jest spełniona przez każdą liczbę rzeczywistą należącą do przedziału <1;3> (x−1)(x−3)<0 Nic wiecej nie napisalem już jak to ruszyć?

Piotr 10: podbijam

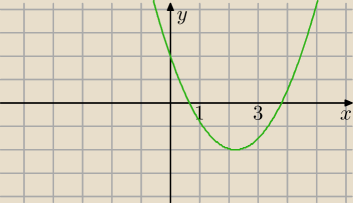
Lorak: przykładowy rysunek. może coś pomoże

ZKS: Warunki jakie muszą być spełnione to f(1) < 0 ∧ f(3) < 0.

pigor: ..., czy odp. to −2< m < ¹₃

ZKS:

	1
Jeżeli ja się nigdzie nie pomyliłem to mi wychodzi m ∊ (0 ;		).
	3

Piotr 10:

	1
Odp to m∊(0;		)
	3

Piotr 10: Tylko ja tak sie zastanawiam, że na tym wykresie co podał Lorak funkcja przyjmuje wartosci ujemne nie tylko w przedziale <1;3> i tego za bardzo nie rozumiem. Nie da sie przeciez narysowac funkcji tej, ktora w przedziale <1;3> przyjmuje tylko wartosci ujemne

ZKS: Ten wykres który podał Lorak to ma być dla Ciebie wskazówka.

pigor: ... , no tak, racja , bo rozwiązanie sprowadza się do alternatywy nierówności : (3m<1 i m+3>3) lub (m+3<1 i 3m>3) ⇔ (m<¹₃ i m>0) lub (m<−2 i m>1) ⇒ ⇔ 0< m< ¹₃ lub m∊∅ ⇔ 0< m< ¹₃ ⇔ m∊(0;¹₃) .

Piotr 10: No tak, czyli z treści zadania mam wnioskować, że ta funkcja w przedziale <1;3> przyjmuje wartośći ujemne, ale też może przyjmować je , np. <0;4> ?

ZKS: Twoja nierówność (x − 3m)(x − m − 3) < 0 ma być spełniona przez wszystkie liczby x ∊ (1 ; 3). Tak więc jeżeli zbiór rozwiązań Twojej nierówności będzie x ∊ (0 ; 4) to w tym zbiorze zawierają się wszystkie liczby ze zbioru x ∊ (1 ; 3) czyli to o co nam chodziło.

Piotr 10: Ale przedzial mam x∊<1;3>, nie rozumiem

Piotr 10: Nie rozumiem dlaczego x=1 i x=3 się wliczają, przecież dla x=1 i x=3 wartosci funkcji wynoszą 0

ZKS: Spokojnie zaczynasz od złej strony podchodzić do tego zadania. Tak mój błąd tam winno być x ∊ [1 ; 3] ale wszystko to co napisałem jest okej.

ZKS: Twoja nierówność (x − 3m)(x − m − 3) < 0 ma być spełniona przez wszystkie liczby x ∊ (1 ; 3). Jak to rozumiesz? Powiedz swoimi słowami.

ZKS: Kurde x ∊ [1 ; 3].

Piotr 10: Chyba wiem w czym u mnie problem tkwił. Od początku sobie wmówiłem, że ta funkcja przyjmuje wartości ujemne w przedziale (1;3). Nie potrafiłem zrozumieć dlaczego x=1 i x=3 jest wliczone. A ta funkcja może przyjmować wartości ujemne, np. x∊(0;10) , ale patrząc na zbiór będzie to x∊<1:3>

ZKS: Tak ten zbiór x ∊ (0 ; 10) zawiera wszystkie liczby ze zbioru x ∊ [1 ; 3] tak więc wszystkie liczby ze zbioru x ∊ [1 ; 3] spełniają Twoją nierówność.

Piotr 10: OK. Dzięki ZKS za pomoc, robię zadania z funkcji kwadratowej, tylko trudne wszystkie dla mnie są , np. tego typu co teraz lub ''Dla jakich wartosci parametru m pierwiastki rownania x²−4(m+1)x+2m(m−1)=0 spelniaja warunek x₁<m<x₂?'' Czarna magia

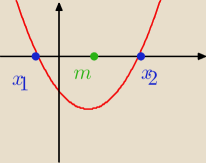
ZKS: Widzisz coś jaki warunek musisz dać?

Piotr 10: Nie wiem, może cos z wierzcholkiem paraboli ? Coś z f(x₁) f(x₂)?

Piotr 10: f(m)<0?

ZKS: Tak. A wiesz dlaczego f(m) < 0?

Piotr 10: Tak wiem jest to funkcja kwadratowa o ramionach skierowanych do góry, miejsca zerowe to przeciecie sie z Osia OX i jezeli x₁<m<x₂ to f(m)<0

Piotr 10: I wynika to jeszcze z rysunku, który podaleś mi

ZKS: Dokładnie. Widzę że rozumiesz już to. Tutaj szczerze mówiąc nawet warunku Δ > 0 nie musimy dawać jeżeli f(m) < 0 wiesz dlaczego?

ZKS: Klucz to jest właśnie zrobienie poglądowego rysunku i wtedy widać wszystko.

Piotr 10: moment pomysle

Piotr 10: Nic mi nie przychodzi do glowy, mozesz powiedziec ?

Piotr 10: Δ>0 dla kazdego m∊R bo Δ=...=8m²+1 tak?

Piotr 10: ZKS jak możesz sprawdź mój wynik, gdyż nie mam odpowiedzi do tego zadania wyszlo mi, że , m∊(−∞;−6)∪ (0;+∞)

ZKS: Ramiona są skierowane do góry i jeżeli ta funkcja dla jakiegoś argumentu m przyjmuje wartość f(m) < 0 to wykres ten przecina w dwóch miejscach oś OX to widać na tym rysunku nawet. Mam nadzieje że rozumiesz.

ZKS: Wygląda .

Piotr 10: Dla jakich wartości parametru m trójmian kwadratowy f(x)=(m−1)x²+2mx+3m−2 jest kwadratem pewnego dwumianu? Jak to ruszyć?

ZKS: No kiedy będzie taka sytuacja pomyśl. Dam Tobie 5 minut na przemyślenie.

Piotr 10: Ok, chwilka muszę koledze zeskanować coś

ZKS: Okej ale zadanie jest na tyle proste że jak wpadniesz na rozwiązanie to aż złapiesz się za głowę.

Piotr 10: Hehe, zadanie z dwoma gwiazdkami to jest

ZKS: Naprawdę? Chyba że trzeba dać najpierw odpowiednie założenie.

Piotr 10: Tak naprawdę . Wzory skroconego mnozenia trzeba uzyc?

ZKS: Raczej nie są potrzebne chyba żeby zauważyć jakie dać odpowiednie założenie.

Piotr 10: Chyba na nic nie wpadne w tym zadaniu

ZKS: Jak byś zapisał inaczej wyraz środkowy ten co zawiera x. Chodzi mi o formę przed wymnożeniem 2 * a * b.

Piotr 10: albo chwilka

Godzio: ax² + bx + c = (√a(x − x₀) )² = a(x − x₀)² A teraz ? Kiedy mamy do czynienia z taką sytuacją ?

Piotr 10: Dażę, aby wspolczynnik a był rowny jeden wtedy m=2 i otrzymuję x²+2x+4=(x+2)² a wiec dla m=2 można tak ?

Godzio: Strzelać każdy może, ale to nie rozwiązanie

Piotr 10: E tam , dazylem do wzoru skroconego mnozenia i zauwazylem ze gdy m=2 to bedzie wszystko gralo

ZKS: No Godzio chyba już podpowiedział najlepiej jak było można.

ZKS:

	1
Przykładowo dla m =		też mamy kwadrat.
	2

Tylko Godzio ciii już teraz nie podpowiadaj.

Piotr 10: ale w odpowiedzi jest , ze m=2 , chyba ze jakis tam blad jest

Godzio:

	1
Właśnie chciałem, żeby sprawdzić
	2

ZKS: Zobacz na wpis który napisał Godzio.

Godzio:

	1
Oj, ale ta		nie będzie pasować, bo będzie coś w stylu −(x − x0)2
	2

ZKS: Godzio nie podpowiadaj.

Piotr 10: Mamy do czynienia z taka sytuacją gdy mamy tylko jedno miejsce zerowe i jest ''ono dwukrotne''

Godzio: Nie podpowiadam przecież

Saizou : W(x)=(m−1)x²+2mx+3m−2 jest to kwadratem pewnego dwumianu, gdy Δ=0 Δ=(2m)²−4(m−1)(3m−2) =−8m²+20m−8=0 ....... m₁=2

	1
m2=
	2

i m≠1

Saizou : to się chyba pospieszyłem

Godzio: Dodajmy a > 0, żeby całość weszła w kwadrat

Piotr 10: Yhym, nic nie szkodzi tak myslalem ze ma byc jedno m₀ post 23:21 czyli będą dwie odpowiedzi ?

ZKS: (m − 1)x² = (√m − 1x)² 3m − 2 = (√3m − 2)² Zobacz jakie tutaj musisz dać warunki.

Godzio:

	1		1		1
Nie, nie, dla m =		mamy (i * (		x −		) )2, więc to chyba jeszcze nie
	2		√2		√2

ten poziom

ZKS: Saizou widzę że wpadł w pułapkę.

Piotr 10: Liczby zespolone widzę , a okej już widzę ZKS 3m−2≥0 i odpada tamta jedna odp

Saizou : jest kwadratem pewnego dwumianu zatem ten w liczbach zespolonych zostaje

ZKS: m − 1 ≥ 0 ∧ 3m − 2 ≥ 0 ⇒ m ∊ [1 ; ∞)

	1
Właśnie dlatego nam m =		odpada.
	2

Saizou : dlatego zawsze trzeba sprawdzić wyniki

Piotr 10: Dobra, ja już idę spać, dzięki Panowie za pomoc . Pozdrawiam

ZKS: Dobra lecę się uczyć. Miłego wieczoru wszystkim.