Wykonaj działania na zbiorach
kamil: Wykonaj działania na zbiorach A,B,X: A u B, A ∩ B, A − B, B −A
A= (0,4) ∪ {5,6,7}
B=(−2,2) ∪ (6,+∞)
Moje wyniki:
AuB = (−2,4) u (6,+∞) , {5,6}
A∩B = (0,2) u {7}
A−B = (2,4) , {5,6,7}
B−A = (−2,0) u (6,+∞)
Czy wszystko robię w porządku?
9 wrz 23:05
5-latek : A zbior X to co to jest za zbior ?
9 wrz 23:09
bezendu: A−B=<2,4>∪{5,6}
B−A=<−2.0>∪(6,∞)/{7}
9 wrz 23:10
9 wrz 23:12
bezendu: pomyłka
A−B=<2,4)∪{5,6}
9 wrz 23:15
kamil: B−A=<−2.0>∪(6,∞)/{7}
rozumiem , ze tutaj chodzi o z wykluczeniem 7?
9 wrz 23:21
bezendu: tak bo w przedziale (6,
∞) zawarta jest 7 a ona należy do zbioru A wiec muszę wykluczyć ja i
daletgo taki zapis
9 wrz 23:24
kamil: Prosiłbym także o pomoc z rozwiązaniem poniżej podanych zbiorów, chciałbym zobaczyć czy mój tok
myślowy jest na dobrej drodze − wszystkie już sam rozwiązałem.
1. A= <0,2> ∪ {−1} , B= (−1,1)
2. A= (−∞,1) ∪ <2,4>, B=(−∞,0) ∪ (3,+∞)
3. A= <−2,3>, B=(−∞,2) ∪ (5,+∞)
9 wrz 23:27
bezendu: Ale podałeś tylko zbiory a nie podałeś co trzeb wyznaczyć ?
9 wrz 23:30
kamil: jeszcze pytanko do bezendu.
dlaczego tutaj "A−B=<2,4)∪{5,6}" dałeś przedział jednostronnie domknięty <2,4)?
9 wrz 23:31
kamil: trzeba wyznaczyć to samo co wyżej:
A u B, A ∩ B, A − B, B −A
9 wrz 23:31
bezendu:
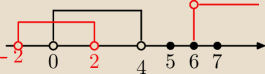
Już Ci pisze
A−B czyli takie które należą do zbioru A a nie należą do zbioru B
<2,4)U{5,6} 4 nie należy do zbioru A wiec nie może być > tylko musi być )
9 wrz 23:37
bezendu:
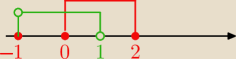
1
A= <0,2> ∪ {−1} , B= (−1,1)
A∪B=<−2,2>
A∩B<0,1)
A\B={−1}∪<1.2>
B\A=(−1,0)
9 wrz 23:40
kamil: 2 należy do zbioru A ( bo była w środku ) dlatego jest <2,4) zamiast (2,4) , dobrze rozumuje?
9 wrz 23:41
bezendu:
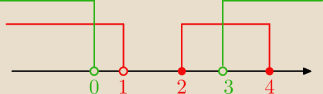
A= (−
∞,1) ∪ <2,4>, B=(−
∞,0) ∪ (3,+
∞)
A∪B=(−
∞,1)∪<2,
∞)
A∩B=(−
∞,0)∪(3,4>
A\B=<0,1)∪<2,3>
B\A=(4,
∞)
9 wrz 23:45
bezendu: Tak, ponieważ 2 należy do zbioru A a nie należy do zbioru B dlatego <
ostatni przykład zrób sam
9 wrz 23:46
kamil: Za chwilę wpiszę
Kilka pytań:
W pierwszym przykładzie nie ma błędu w tym A∪B=<−2,2> ?
Powinno być <−1,2> ?
Rozumiem, że tutaj zamknięty przy −1, ponieważ punkt na osi {−1} traktujemy jako zamknięty ze
zbioru A?
9 wrz 23:52
bezendu: tak masz racje −1 nie wiem skąd ja wziąłem −2
9 wrz 23:54
bezendu:
@Kamil ja idę spać zobaczę jurto rano albo ktoś inny Ci sprawdzi
9 wrz 23:55
kamil:
A∪B= (−
∞,3> ∪ (5,+
∞)
A∩B= <−2,2)
A−B= <2,3>
B−A=(−
∞,−2) ∪ (5,+
∞)
10 wrz 00:08
kamil: sprawdzi ktos?
10 wrz 19:07
bezendu: ok
10 wrz 19:11
kamil: Czy ktoś mógłby sprawdzić poprawność zadania?
A= {xεN:x+3>8}
B= {xεN:x−7≤6}
AuB= {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15...}
A∩B= {6,7,8,9,10,11,12,13}
A−B= {14,15,16,17,18...}
B−A= {1,2,3,4,5}
Czy w takich zbiorach trzeba gdzieś dopisywać, że zbiór należy do N? Czy wystarczy rozwiązywać?
Pominąłem całość zadania, ponieważ już trochę późno
11 wrz 00:41
kamil: up
11 wrz 18:22