Geometria, równanie okręgu Magda: Napisz równanie okręgu stycznego do osi x i osi y oraz stycznego zewnętrznie do okręgu o równaniu (x−8)² + (y−8)² = 64 Mógłby ktoś pomóc? Kompletnie tego nie rozumiem

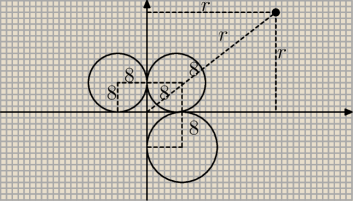
irena_1: Dany okrąg ma środek w punkcie (8, 8) i promień równy 8. O₁: (x+8)²+(y−8)²=64 O₂: (x−8)²+(y+8)²=64 r+16=r√2 r(√2−1)=16 r=16(√2+1) O₃: (x−16√2−1)²+(y−16√2−1)²=256(3+2√2)

Magda: odpowiedzi to (x − 24 +16√2)² + (y−24 + 16√2)² =64(17 −12√2)

Magda: potrafi ktoś poprawnie rozwiązać?

irena_1: Oj, widzę, co pominęłam. r√2=r+8+8√2 r(√2−1}=8(√2+1) r(2−1)=8(√2+1)(√2+1) r=8(3+2√2)=24+16√2 r²=64(9+12√2+8)=64(17+12√2) O₃: (x−24−16√2)²+(y−24−16√2)²=64(17+12√2) R√2=8√2−8−R R{√2+1)=8(√2−1) R=8(√2−1)²=8(3−2√2) R²=64(17−12√2) O₄: (x−24+16√2)²+(y−24+16√2)²=64(17−12√2)

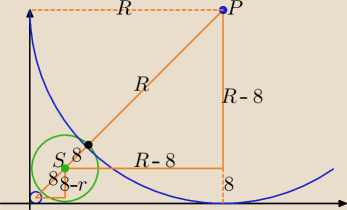
Bogdan: Są 2 rozwiązania: okrąg mniejszy o promieniu r i okrąg większy o promieniu R S = (r, r) to środek mniejszego okręgu stycznego do osi x i y i zewnętrznie do danego okręgu P = (R, R) to środek większego okręgu stycznego do osi x i y i zewnętrznie do danego okręgu Mniejszy okrąg: 8 + r = √2(8 − r) Większy okrąg: 8 + R = √2(R − 8)

Bogdan: Trzeba oczywiście rozwiązać równania i obliczyć r oraz R

irena_1: Są 4 rozwiązania− w II i IV ćwiartce również