Funkcja bezendu:

	x1+x2
Wyznacz dziedzinę i naszkicuj wykres funkcji f danej wzorem f(m)=		gdzie x1 i x2
	2

są różnymi pierwiastkami równania (m+2)x²+(m²+2m)x+m²=0 Δ=(m²+2m)²−4m²(m+2) m⁴+4m³+4m²−4m³−8m²=0 m⁴−4m²=0 m²(m²−4)=0 m²(m−2)(m+2)=0 m=0 lub m=2 lub m=−2∉D dalej nie wiem co zrobić ?

ZKS: Aby istniały dwa różne pierwiastki jakie musisz dać warunki?

bezendu: Δ>0

ZKS: Tylko?

Piotr: a ≠ 0 i Δ > 0 ? heh dawno tego nie robilem

bezendu: Tak, nie mam podane że mają być tych samych znaków albo przeciwnych

Piotr: gdy a = 0 to masz tylko 1 pierwiastek

bezendu: Piotr chyba jednak nie, mam podane że D=R\{−2} m+2≠0 m≠−2

ZKS:

ZKS: Piotr napisał dobrze.

bezendu: ZKS czyli moja wersja czy Piotra ?

Piotr: no tak , gdy masz − 2 to bedzie tylko jeden pierwiastek i dlatego wypada z dziedziny. no tak mysle

bezendu: m∊(−∞,−2)∪(2,∞)

ZKS: Piotr dla m = −2 mamy równanie sprzeczne.

Piotr: faktycznie

ZKS: bezendu czyli z warunku Δ > 0 ∧ a ≠ 0 masz że m ∊(−∞ ; −2) ∪ (2 ; ∞).

ZKS: To jest Twoja dziedzina.

bezendu: No tak a dalej ?

ZKS: Zapisz jak wygląda Twoja funkcja f(m).

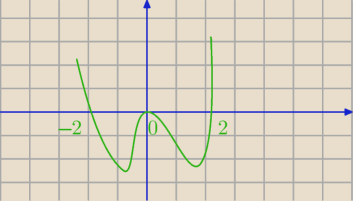
Mila: To jak jest oryginalna treść zadania? Bezendu, a wykres f(m)?

bezendu: Mila Tak to jest oryginalna wersja zadania.

ZKS: Jak wygląda funkcja f(m)?

bezendu: Właśnie nie wiem jak określić ten wzór

ZKS: Znasz wzory Viete'a?

bezendu: znam

bezendu:

	1
f(m)=−		m
	2

ZKS:

bezendu: Dziękuje za pomoc

ZKS: Nie ma za co proszę bardzo.