geometria
zadanie: Niech P(α, β, γ) bedzie polem trójkata wpisanego w okrag o promieniu 1, majacego katy α, β, γ.
Czy wtedy
a) P(30�o, 60o�, 90�o)<P(20o�, 70o�, 90o�) ?
zrobilem tak:
korzystajac ze wzoru 2R2*sinα*sinβ*sinγ mam:
P(30�o, 60o�, 90�o)=2sin30o*sin60o=sin60o
P(20o�, 70o�, 90o�)=2sin20o*sin70o=2sin20o*cos20o=sin40o
stad sin60o>sin40o czyli nierownosc jest nieprawdziwa dobrze? mozna inaczej to zrobic?
prosciej?
9 wrz 18:38
PW: Prościej: zauważyć, że skoro w obu trójkątach jest kąt o mierze 90°, to oba mają
przeciwprostokątną równą średnicy okręgu.. Zauważyć, że pole takiego trójkąta liczone jako
| | 1 | |
|
| ch (c − długość przeciwprostokątnej, h − wysokość opuszczona na przeciwprostokątną) |
| | 2 | |
jest funkcją zmiennej α (α − miara jednego z kątów ostrych, załóżmy że α≤β).
Określona w ten sposób funkcja P(α), α∊(0,45°) jest rosnąca, a więc P(20°<P(30°).
Nie wiem czy to jest prościej. Dla mnie tak, bo im większy α, tym większa wysokość h. Wystarczy
narysować. Trójkąty umieścić tak jak jest wygodnie − niech maja wspólną przeciwprostokątną i
niech leżą w tym samym półkolu (położenie nie wpływa na pole)
9 wrz 19:08
Mila:
Wygląda, że dobrze.
Możesz inaczej, nie korzystać z tego wzoru, (możesz go zapomnieć) np. obliczyć a i b ( znasz
przeciwprostokątną: c=2)
Wtedy porównujesz ... dokończ
9 wrz 19:11
zadanie:
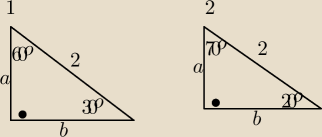
1 trojkat
a=1
b=
√3
2 trojkat
a=2sin20
o
b=2cos20
o
P=2sin20
o*cos20
o=sin40
o
wyszlo to samo
10 wrz 10:58
PW: A dlaczego założyłeś, że a=1? To nieprawda.
10 wrz 11:11
10 wrz 11:14
PW: No dobrze, to prowokacja, Ale skąd tak od razu widzisz, że a=1 w pierwszym trójkącie?
10 wrz 11:18
PW: Za wolno piszę.
Czyli w drugim trójkącie nie da się tak jasno zrealizować pomysłu Mili?
10 wrz 11:20
zadanie: mozna to obliczyc tak jak wyzej albo ze zwiazkow w trojkacie o katach 30o, 60o, 90o
10 wrz 11:20
zadanie: no dokladnie nie da sie obliczyc dlugosci tych bokow bo nie znam dokladnej wartosci sin20o i
cos20o
10 wrz 11:23
zadanie: a jak bedzie tak:
b) P(30
o, 60
o, 90
o)<P(30
o, 50
o, 100
o)
| | √3 | |
Pole pierwszego trojkata sie nie zmienia P=sin60o= |
| |
| | 2 | |
a pole drugiego? to juz nie jest trojkat prostokatny
obliczajac z tego wzoru na poczatku byloby tak:
P
2=sin50
o*sin80
o
ale teraz mam problem z porownaniem czy sin60
o<sin50
o*sin80
o ?
10 wrz 11:30
PW: No, tu zaczynają się problemy, nie jest to oczywiste.
10 wrz 11:50
PW: sin60°>sin50°
Popomnożeniu przez dodatnie sin80°
sin60°sin80°>sin50°sin80°
sin80°<1, więc
sin60°>sin60°sin80°>sin50°sin80°
takich rzeczy nie ćwiczą w szkole.
10 wrz 12:00
zadanie: ok dziekuje
10 wrz 12:08
Mila:
No,pieknie.
Wyprowadź wzór na pole Δ;
PΔ= 2R2*sinα*sinβ*sinγ , gdzie R, α,β,γ to dane jak w pierwszym zadaniu, a trójkąt jest
dowolny.
10 wrz 15:46
zadanie: ale co pieknie? ze dobrze czy ze zle?
10 wrz 15:49
Mila:
Rozwiązujesz z PW, to musi być dobrze.
Korzystałeś z wzoru, który podałam 15:46, więc wyprowadź, bo łatwo i może się przydać.
10 wrz 15:51
zadanie: slyszalem, ze PW jest nauczycielem
10 wrz 15:57
zadanie: sprobuje wyprowadzic ten wzor
10 wrz 15:57
Mila: Do zobaczenia na forum po 20. Powodzenia . ( skorzystaj z tw. sinusów)
10 wrz 16:30
zadanie: wiem wlasnie tez na to wpadlem
10 wrz 16:33
zadanie:
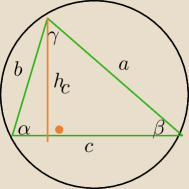
10 wrz 16:49
zadanie: Z tw, sinusow:
| | 1 | |
P= |
| *2Rsinγ*2Rsinα*sinβ=2R2*sinα*sinβ*sinγ |
| | 2 | |
10 wrz 16:53
Mila: 
10 wrz 21:14
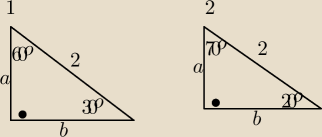 1 trojkat
a=1
b=√3
1 trojkat
a=1
b=√3

