Jednokładność
Jaro9: W dany trójkąt równoboczny ABC wpisz trójkąt równoboczny, którego odpowiednie boki są
prostopadłe do odpowiednich boków danego trójkąta.
Wskazówka:
Z dowolnego punktu D∊AC poprowadź prostą prostopadłą do boku AB. Oznacz przez E punkt, w którym
przetnie ona ten bok. Skonstruuj pomocniczy trójkąt równoboczny DEF i rozważ odpowiednią
jednokładność.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Jak wiadomo szukany trójkąt równoboczny to będzie taki, gdzie wierzchołki tego trójkąta
| | 1 | |
znajdują się na |
| boku. Ale chcę wykonać to zadanie przy użycia cyrkla i linijki bez |
| | 3 | |
podziałki korzystając z jednokładności, twierdzenia Talesa.
Problem polega na tym, aby wskazać odpowiednią jednokładność. Brakuje mi chociaż jednego punktu
szukanego trójkąta o który mógłbym się "zaczepić".
Mila:
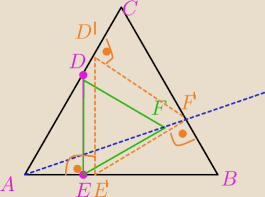
DE⊥AB
rysujesz półprostą AF, masz wyznaczony jeden z wierzchołków (F' )szukanego ΔD'E'F'.
Pozostałe wierzchołki wyznaczasz rysując F'D' równoległą do DF, następnie D'E' równoległą do
DE.
D'E'⊥AB
E'F' ⊥BC
D'F' ⊥ AC
