okrag aaa: Dany jest okrąg o₁ o równaniu x² + y² + 6x + 5 = 0 oraz okrąg o₂ o równaniu x² + y² − 12x + 8y+ 27 = 0 . Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu o₁ jest okrąg o2 .

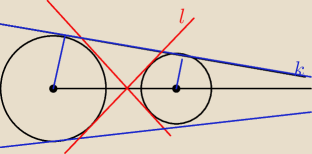
Basia: 1. wyznacz S₁, r₁ i S₂,r₂ 2. napisz równanie pr. S₁S₂ 3. napisz równania stycznych do obu okręgów będą cztery rozwiązania

	r1
4. znajdź punkt wspólny pr.S1S2 i k s1 =
	r2

	r1
5. znajdź punkt wspólny pr.S1S2 i l s2 = −
	r2

myślę jeszcze czy można znaleźć prostszy sposób

Saizou : albo z definicji jednokładności

Basia: obrazem o₁ ma być o₂ (nie doczytałam) czyli skale trzeba odwrócić

	r2
s = ±
	r1

Basia: oczywiście, że jest prostszy sposób O₁ punkt przecięcia niebieskich ⇒

	r2
O1S2→ =		*O1S1→
	r1

z tego wyznaczymy O₁ O₂ punkt przecięcia czerwonych

	r2
O2S2→ = −		*O2S1→
	r1

z tego wyznaczymy O₂

aaa: dziekuję ale tych współrzędnych środka jednokładności i tak nie rozumiem

aaa: a takie cos: W pewnej klasie okazało się, że są 3 osoby, które urodziły się w kwietniu tego samego roku i są dwie osoby, które urodziły się w lipcu tego samego roku. Oblicz prawdopodobieństwo, że troje z tych 5 uczniów urodziło się tego samego dnia roku.

Basia: na pewno dobrze przepisałeś ? i kompletnie ? jeżeli tak, to oczywiście tylko ci z kwietnia mogą być brani pod uwagę kwiecień ma 30 dni czyli mamy: 3→30 czyli 30³ możliwości

	30		1		1
P =		=		=
	303		302		900