dana jest funkcja
stilla sanguinis: f(x)=||x|−1|
spr. czy funkcja
1. ma dwa ekstrema
2. jest ciągła w swojej dziedzinie
3. ma dokładnie 1 miejsce zerowe
4. f(−2)=−1
póki co doliczyłam się i " dorysowałam"

że funkcja 2. jest ciagła w swej dziedzinie a więc
ten podpunkt oznacze jako prawde, oraz że 3. jest nieprawdziwa doliczyłam się dwóch miejsc
zerowych x=1 i x=−1
punkt 4 wyszedł mi nieprawdziwy po podstawieniu −2 za x−sa wyszlo mi 1
pytanie czy te punkty mam dobrze zrobione, oraz jak policzyć ekstrema jeśli funkcja ma
moduł→→jak policzyc pochodna z modulem?
7 wrz 19:31
sushi_ gg6397228:
zrobić rysunek i po sprawie
7 wrz 19:51
stilla sanguinis: a co jeśli w module będzie o wiele bardziej skomplikowana funkcja? wtedy przydałaby mi się
znajomość liczenia pochodnych z modułem
wyjaśni mi ktoś jak to zrobić?
7 wrz 19:53
stilla sanguinis: no i pytanie czy podalam poprawne odp dla punkttu 2,3 i 4?
7 wrz 19:57
Eta:
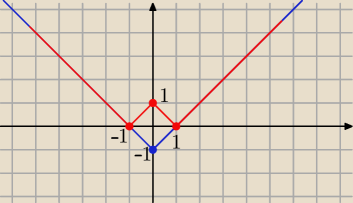
7 wrz 20:00
sushi_ gg6397228:
jak bedzie brzydko pod modułem , to trzeba bedzie rozbić na kilka funkcji i potem sobie
policzyc
jak zrobisz rysunek, to bedzie wiadomo czy odp2,3,4 sa ok czy trzeba cos zmienic
7 wrz 20:03
stilla sanguinis: tak już zapytam dla pewności funkcja będzie miała dwa ekstrema co nie?
7 wrz 20:08
 że funkcja 2. jest ciagła w swej dziedzinie a więc
ten podpunkt oznacze jako prawde, oraz że 3. jest nieprawdziwa doliczyłam się dwóch miejsc
zerowych x=1 i x=−1
punkt 4 wyszedł mi nieprawdziwy po podstawieniu −2 za x−sa wyszlo mi 1
pytanie czy te punkty mam dobrze zrobione, oraz jak policzyć ekstrema jeśli funkcja ma
moduł→→jak policzyc pochodna z modulem?
że funkcja 2. jest ciagła w swej dziedzinie a więc
ten podpunkt oznacze jako prawde, oraz że 3. jest nieprawdziwa doliczyłam się dwóch miejsc
zerowych x=1 i x=−1
punkt 4 wyszedł mi nieprawdziwy po podstawieniu −2 za x−sa wyszlo mi 1
pytanie czy te punkty mam dobrze zrobione, oraz jak policzyć ekstrema jeśli funkcja ma
moduł→→jak policzyc pochodna z modulem?
